
若曲线f(x)=acosx与曲线g(x)=x2+bx+1在交点(0,m)处有公切线,则a+b=( )
A.-1 B.0
C.1 D.2
科目:高中数学 来源: 题型:
设等差数列{an}的前n项和是Sn,且a1=10,a2= 9,那么下列不等式中不成立的是( )
9,那么下列不等式中不成立的是( )
A.a10+a11>0 B.S21<0
C.a11+a12<0 D.n=10时,Sn最大
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}中,a1=2,a8=4,f(x)=x(x-a1)(x-a2)…(x-a8),f ′(x)为函数f(x)的导函数,则f ′(0)=( )
A.0 B.26
C.29 D.212
查看答案和解析>>
科目:高中数学 来源: 题型:
给出定义:若函数f(x)在D上可导,即f ′(x)存在,且导函数f ′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f ″(x)=(f ′(x))′.若f ″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,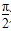 )上不是凸函数的是________(把你认为正确的序号都填上).
)上不是凸函数的是________(把你认为正确的序号都填上).
①f(x)=sinx+cosx; ②f(x)=lnx-2x;
③f(x)=-x3+2x-1; ④f(x)=xex.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取到极小值
B.当k=1时,f(x)在x=1处取到极大值
C.当k=2时,f(x)在x=1处取到极小值
D.当k=2时,f(x)在x=1处取到极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的导函数为f ′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
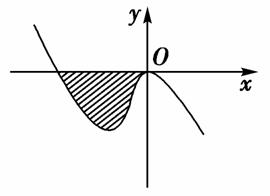
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为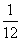 ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com