
【题目】已知函数![]() .
.
(1)求证:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)当![]() 时,若
时,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,试讨论函数
,试讨论函数![]() 的零点情况.
的零点情况.
【答案】(1)答案见解析(2)![]() (3)答案见解析
(3)答案见解析
【解析】
(1)根据函数单调性的定义证明,即可求得答案;
(2)设![]() ,当
,当![]() 时,
时,![]() 恒成立,得到关于
恒成立,得到关于![]() 的不等式组,即可求得答案;
的不等式组,即可求得答案;
(3)求出![]() 的值域,问题转化为求方程
的值域,问题转化为求方程![]() 的实数根,令
的实数根,令![]() ,得到方程
,得到方程![]() ,求出
,求出![]() 的值,通过讨论
的值,通过讨论![]() 的范围,即可求得答案.
的范围,即可求得答案.
(1)设![]() 是
是![]() 上的任意两个数,且
上的任意两个数,且![]() ,则
,则![]()
则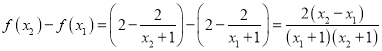
![]()
![]() ,
,![]()
![]()
![]()
即![]()
![]()
![]() 在
在![]() 上递增;
上递增;
(2)![]() ,即
,即![]()
设![]()
![]()
![]()
![]()
![]()
即当![]() 时,
时,![]() 恒成立,
恒成立,
![]()
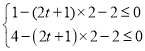 ,
,
解得:![]()
![]() 实数
实数![]() 的范围是
的范围是![]()
(3)![]()
![]() x>0,则
x>0,则![]()
![]()
![]() ,
,
即![]() ,
,
当![]() 时,由(1)得
时,由(1)得![]() 递增,
递增,![]() 递增,
递增,
![]()
![]() 递增,
递增,
![]()
![]() g(x)的值域是
g(x)的值域是![]() ,
,
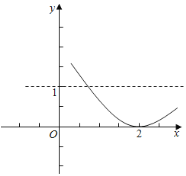
![]()
![]() 的大致图象如图示:
的大致图象如图示:
 ,
,
![]() 函数
函数![]() 的零点
的零点
![]() 方程
方程![]() 的实数根,
的实数根,
令![]() ,即
,即![]()
解得:![]() 或
或![]() ,
,
![]() 时,满足条件的实数根有且只有一个,
时,满足条件的实数根有且只有一个,
![]()
![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 有
有![]() 个零点,
个零点,
当![]() ,即
,即![]() 时,函数
时,函数![]() 只有
只有![]() 个零点,
个零点,
当![]() ,即
,即![]() 时,函数F(x)有
时,函数F(x)有![]() 个零点,
个零点,
综上所述,![]() 时,函数
时,函数![]() 只有
只有![]() 个零点,
个零点,
![]() 时,函数
时,函数![]() 有
有![]() 个零点,
个零点,
![]() 时,函数
时,函数![]() 有
有![]() 个零点.
个零点.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)讨论函数![]() 在定义域内极值点的个数;
在定义域内极值点的个数;
(3)设直线![]() 为函数
为函数![]() 的图象上一点
的图象上一点![]() 处的切线,证明:在区间
处的切线,证明:在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
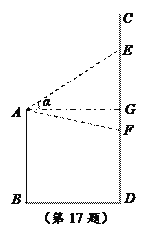
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮(如图1阴影部分),并卷成一个深度为![]() 米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为
米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为![]() .
.
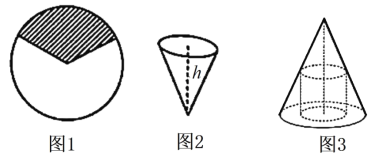
(1)求圆锥筒的容积;
(2)在(1)中的圆锥内有一个底面圆半径为![]() 的内接圆柱(如图3),求内接圆柱侧面积最大时
的内接圆柱(如图3),求内接圆柱侧面积最大时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式![]() .
.
(1)是否存在实数m,使不等式对任意![]() 恒成立?并说明理由.
恒成立?并说明理由.
(2)若不等式对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)若对于![]() ,不等式恒成立,求实数x的取值范围.
,不等式恒成立,求实数x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com