练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在直三棱柱ABC—A1B1C1中，∠ACB=90°，B1B=BC=CA=4，D1是A1B1中点E是BC1的中点，BD1交AB1于点F

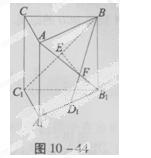
    （1）求证：AB1⊥BC1；

    （2）求二面角B—AB1—C的大小；

    （3）求点C到平面BEF的距离。


    （3）答案：(解法一) ∵E为B1C的中点，∴C到平面BEF的距离等于B1到平面BEF的距离，∵ABC-A1B1C1为直棱柱，A1C1=B1C1，D1为中点，∴C1D1⊥A1B1，∴C1D1平面A1B1BA，∴CD1⊥B1F，又由（2）知

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某学生在体育训练时弄伤了膝关节，医生给开了一些消炎药，并嘱咐每天早晚8点各服用一片药片，已知该药品每征220mg,他的贤脏每次12小时从体内滤出这种药的60%，如果这种药在体内残留超过386mg,将产生副作用。

    请问：（1）该同学上午8时第一次服药后，到第二天早晨服药后，药在体内还残留多少？

    （2）该同学若长期服用该药，会不会产生副作用？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆的半径为，圆心在直线上，圆被直线截得的弦长为，则圆的标准方程为                                                   

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知是两条不同直线，是三个不同平面，下列命题中正确的是（    ）

    A．       B． 

    C．          D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


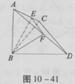
    如图，正三棱柱ABC—A1B1C1底面边长为a，侧棱长为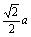，D是A1C1的中点。

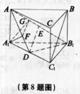
    （1）求证：BC1∥平面B1DA；

    （2）求证：平面AB1D⊥平面A1ACC1；

    （3）求二面角A1—AB1—D的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-19，在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=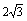，M、N分别为AB、SB的中点

    （1）证明：AC⊥SB；

    （2）求二面角N-CM-B的大小。

    （3）求点B到平面CMN的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-18，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点且BF⊥平面ACE。

       

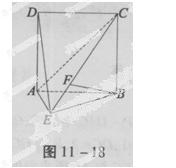
    （1）求证：AE⊥平面BCE；

    （2）求二面角B-AC-E的大小；

    （3）求点D到平面ACE的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在三棱柱ABC-A1B1C1中，A1在底面上的射影在线段AC上，底面△ABC是以∠B为直角的等腰三角形，M为AC的中点，又AB=AA1=a

    （1）求证：BM⊥AA1；

    （2）若A1C⊥平面BMC1，求证：三棱柱ABC-A1B1C1为直三棱柱。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个空间几何体的三视图如图所示，则该几何体的表面积为（    ）

       A． 48          B．           C．      D．80

    查看答案和解析>>

    同步练习册答案