考点:直线与平面平行的判定,直线与平面垂直的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)先根据线面垂直的性质证明出BB1⊥A1C1.进而根据菱形的性质证明出A1C1⊥B1D1.最后根据线面垂直的判定定理证明出A1C1⊥平面B1BDD1.
(Ⅱ)连接AC,交BD于点E,连接C1E.先证明OC1∥AE和OC1=AE,推断出AOC1E为平行四边形,进而推断AO∥C1E,最后利用线面平行的判定定理证明出AO∥平面BC1D.
(Ⅲ)先由E为BD中点,推断出BD⊥C1E,进而根据C1D=C1B,推断出ME⊥BD,进而根据OM⊥BD,推断出BD∥B1D1.直角三角形OC1E中利用射影定理求得OM.
解答:
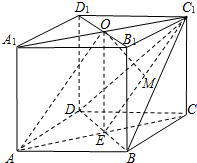
解:(Ⅰ)依题意,因为四棱柱ABCD-A
1B
1C
1D
1中,AA
1⊥底面ABCD,
所以BB
1⊥底面A
1B
1C
1D
1.
又A
1C
1?底面A
1B
1C
1D
1,
所以BB
1⊥A
1C
1.
因为A
1B
1C
1D
1为菱形,
所以A
1C
1⊥B
1D
1.而BB
1∩B
1D
1=B
1,
所以A
1C
1⊥平面B
1BDD
1.
(Ⅱ)连接AC,交BD于点E,连接C
1E.
依题意,AA
1∥CC
1,
且AA
1=CC
1,AA
1⊥AC,
所以A
1ACC
1为矩形.
所以OC
1∥AE.
又
OC1=A1C1,
AE=AC,A
1C
1=AC,
所以OC
1=AE,所以AOC
1E为平行四边形,
则AO∥C
1E.
又AO?平面BC
1D,C
1E?平面BC
1D,
所以AO∥平面BC
1D.
(Ⅲ)在△BC
1D内,满足OM⊥B
1D
1的点M的轨迹是线段C
1E,包括端点.
分析如下:连接OE,则BD⊥OE.
由于BD∥B
1D
1,故欲使OM⊥B
1D
1,只需OM⊥BD,从而需ME⊥BD.
又在△BC
1D中,C
1D=C
1B,又E为BD中点,所以BD⊥C
1E.
故M点一定在线段C
1E上.
当OM⊥C
1E时,OM取最小值.
在直角三角形OC
1E中,OE=1,
OC1=,
C1E=,
所以
OMmin==.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用.考查了学生基础知识的综合运用.

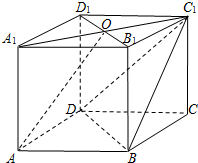 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1 解:(Ⅰ)依题意,因为四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,
解:(Ⅰ)依题意,因为四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,

 名校课堂系列答案
名校课堂系列答案 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为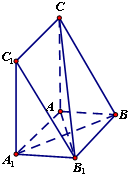 如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.
如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.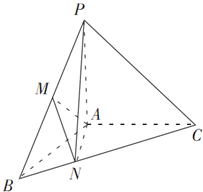 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=