
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ②若
②若![]() ,则
,则![]()
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]()
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (其中
(其中![]() 为常数),若函数
为常数),若函数![]() 在区间
在区间![]() 上不存在极值,且存在
上不存在极值,且存在![]() 满
满
足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区客栈的工作人员为了控制经营成本,减少浪费,合理安排入住游客的用餐,他们通过统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)若入住客栈的游客人数![]() 与月份
与月份![]() 之间的关系可用函数
之间的关系可用函数![]() (
(![]() ,
, ![]() ,
, ![]() )近似描述,求该函数解析式;
)近似描述,求该函数解析式;
(2)请问哪几个月份要准备不少于400人的用餐?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某汽车品牌一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如下:
的概率分布如下:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)假设一月与二月被消费者投诉的次数互不影响,求该汽车品牌在这两个月内被消费者投诉![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E,F在圆O上,且AB//EF,AB=2EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.
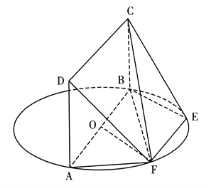
(I)证明:OF//平面BEC;
(Ⅱ)证明:平面ADF![]() 平面BCF.
平面BCF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com