练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    （1）若，求函数的零点；

    （2）若在恒成立，求的取值范围；

    （3）设函数，解不等式.

    【答案】(1)1；(2) (3)见解析

    【解析】

    （1）解方程可得零点；

    （2）恒成立，可分离参数得，这样只要求得在上的最大值即可；

    （3）注意到的定义域，不等式等价于，这样可根据与0，1的大小关系分类讨论．

    （1）当时，

    令得，，∵，∴函数的零点是1

    （2）在恒成立，即在恒成立，

    分离参数得：，

    ∵，∴

    从而有：.

    （3）

    令，得，，

    因为函数的定义域为，所以等价于

    （1）当，即时，恒成立，原不等式的解集是

    （2）当，即时，原不等式的解集是

    （3）当，即时，原不等式的解集是

    （4）当，即时，原不等式的解集是

    综上所述：当时，原不等式的解集是

    当时，原不等式的解集是

    当时，原不等式的解集是

    当时，原不等式的解集是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0）过点M（m，2），其焦点为F，且|MF|=2．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）设E为y轴上异于原点的任意一点，过点E作不经过原点的两条直线分别与抛物线C和圆F：（x﹣1）2+y2=1相切，切点分别为A，B，求证：直线AB过定点F（1，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）
    A.命题“?x∈R，2x＞0”的否定是“?x0∈R，2 ＜0”
    B.命题“若sinx=siny，则x=y”的逆否命题为真命题
    C.若命题p，￢q都是真命题，则命题“p∧q”为真命题
    D.命题“若△ABC为锐角三角形，则有sinA＞cosB”是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】交通指数是指交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，记交通指数为，其范围为，分别有五个级别：，畅通；，基本畅通；，轻度拥堵；，中度拥堵；，严重拥堵.在晚高峰时段（），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示.

    (1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数；

    (2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；

    (3)从(2)中抽取的6个路段中任取2个，求至少有1个路段为轻度拥堵的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形， ， ， 垂直于底面， ， ， 分别为， 的中点．

    （Ⅰ）求证： ；

    （Ⅱ）求四棱锥的体积和截面的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某销售公司拟招聘一名产品推销员，有如下两种工资方案：

    方案一：每月底薪2000元，每销售一件产品提成15元；

    方案二：每月底薪3500元，月销售量不超过300件，没有提成，超过300件的部分每件提成30元．

    （1）分别写出两种方案中推销员的月工资（单位：元）与月销售产品件数的函数关系式；

    （2）从该销售公司随机选取一名推销员，对他（或她）过去两年的销售情况进行统计，得到如下统计表：

    月销售产品件数

    300

    400

    500

    600

    700

    次数

    2

    4

    9

    5

    4

    把频率视为概率，分别求两种方案推销员的月工资超过11090元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为的学生成绩样本，得频率分布表如下：

    组号

    分组

    频率

    频数

    第一组

    第二组

    ①

    第三组

    ②

    第四组

    第五组

    合计

    （1）写出表中①、②位置的数据；

    （2）估计成绩不低于分的学生约占多少；

    （3）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取名学生进行第二轮考核，分别求第三、四、五各组参加考核的人数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在矩形中,E为的中点，将沿翻折到的位置,平面,为的中点,则在翻折过程中，下列结论正确的是( )

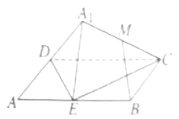
    A.恒有 平面

    B.B与M两点间距离恒为定值

    C.三棱锥的体积的最大值为

    D.存在某个位置，使得平面⊥平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知是递增数列，其前项和为，，且，．

    （Ⅰ）求数列的通项；

    （Ⅱ）是否存在使得成立？若存在，写出一组符合条件的的值；若不存在，请说明理由；

    （Ⅲ）设，若对于任意的，不等式

    恒成立，求正整数的最大值．

    查看答案和解析>>

    同步练习册答案