
已知函数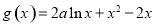 .
.
(1)当 时,讨论函数
时,讨论函数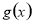 的单调性;
的单调性;
(2)当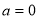 时,在函数
时,在函数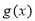 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为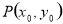 ,试探究函数
,试探究函数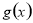 在Q
在Q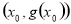 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?
(3)试判断当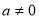 时
时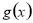 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.
(1)函数 在定义域
在定义域 上单调递增;(2)函数在Q点处的切线与直线AB平行;
上单调递增;(2)函数在Q点处的切线与直线AB平行;
(3) 图象不存在不同的两点A、B具有(2)问中所得出的结论.
图象不存在不同的两点A、B具有(2)问中所得出的结论.
【解析】
试题分析:(1)求导即可知其单调性;(2)利用导数求出函数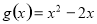 在点Q
在点Q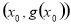 处的切线的斜率,再求出直线AB的斜率,可看出它们是相等的,所以函数在Q点处的切线与直线AB平行;
处的切线的斜率,再求出直线AB的斜率,可看出它们是相等的,所以函数在Q点处的切线与直线AB平行;
(3)设
 ,若
,若 满足(2)中结论,则有
满足(2)中结论,则有
 ,化简得
,化简得 (*).如果这个等式能够成立,则存在,如果这个等式不能成立,则不存在.设
(*).如果这个等式能够成立,则存在,如果这个等式不能成立,则不存在.设 ,则*式整理得
,则*式整理得 ,问题转化成该方程在
,问题转化成该方程在 上是否有解.再设函数
上是否有解.再设函数 ,下面通过导数即可知方程
,下面通过导数即可知方程 在
在 上是否有解,从而可确定函数
上是否有解,从而可确定函数 是否满足(2)中结论.
是否满足(2)中结论.
(1)由题知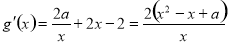 ,
,
因为 时,
时, ,函数
,函数 在定义域
在定义域 上单调递增; 4分
上单调递增; 4分
(2)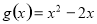 ,
, ,
,

所以函数Q点处的切线与直线AB平行; .7分
(3)设
 ,若
,若 满足(2)中结论,有
满足(2)中结论,有
 ,即
,即
即 (*) .9分
(*) .9分
设 ,则*式整理得
,则*式整理得 ,问题转化成该方程在
,问题转化成该方程在 上是否有解; 11分
上是否有解; 11分
设函数 ,则
,则 ,所以函数
,所以函数 在
在 单调递增,即
单调递增,即 ,即方程
,即方程 在
在 上无解,即函数
上无解,即函数 不满足(2)中结论. 14分
不满足(2)中结论. 14分
考点:导数的应用.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
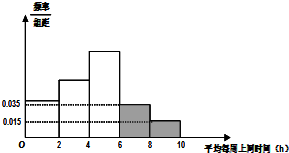 为了解高中生平均每周上网玩微信,刷微博,打游戏享受智能手机带来的娱乐生活体验,从高三年级学生中抽取部分同学进行调查,将所得的数据整理如下,画出频率分布直方图(如图),其中频率分布直方图从左至右前3个小组的频率之比为1:3:5,第二组的频数为150,则被调查的人数应为( )
为了解高中生平均每周上网玩微信,刷微博,打游戏享受智能手机带来的娱乐生活体验,从高三年级学生中抽取部分同学进行调查,将所得的数据整理如下,画出频率分布直方图(如图),其中频率分布直方图从左至右前3个小组的频率之比为1:3:5,第二组的频数为150,则被调查的人数应为( )| A、600 | B、400 |
| C、700 | D、500 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三第六期3月阶段性考试文科数学试卷(解析版) 题型:选择题
已知函数 (
( ),则( )
),则( )
A. 必是偶函数 B.当
必是偶函数 B.当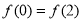 时,
时, 的图象必须关于
的图象必须关于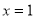 直线对称;
直线对称;
C. 有最大值
有最大值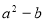 D. 若
D. 若 ,则
,则 在区间
在区间 上是增函数;
上是增函数;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟理科数学试卷(解析版) 题型:选择题
已知复数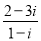 (
(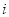 是虚数单位),它的实部与虚部的和是( )
是虚数单位),它的实部与虚部的和是( )
A.4 B.6 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟文科数学试卷(解析版) 题型:解答题
已知函数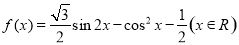
(1)当 时,求函数
时,求函数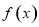 取得最大值和最小值;
取得最大值和最小值;
(2)设锐角 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是 ,且
,且 ,若向量
,若向量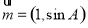 与向量
与向量 平行,求
平行,求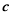 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com