Question

抛物线C的方程为y=ax²(a＜0),过抛物线C上一点P(x₀,y₀)(x₀≠0)作斜率为k₁、k₂的两条直线分别交抛物线C于A(x₁,y₁)、B(x₂,y₂)两点(P、A、B三点互不相同),且满足k₂+λk₁=0(λ≠0且λ≠-1).

(1)求抛物线C的焦点坐标和准线方程;

(2)设直线AB上一点M,满足,证明线段PM的中点在y轴上;

(3)当λ=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标y₁的取值范围.

Answer 1

(1)解:抛物线C的标准方程x²=y,

∴焦点坐标为(0,),准线方程为y=-.

(2)证明:设PA:y-y₀=k₁(x-x₀),PB:y-y₀=k₂(x-x₀),点P(x₀,y₀)和点A(x₁,y₁)的坐标是方程组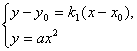的解,消元后化为

ax²-k₁x+k₁x₀-y₀=0,于是x₁+x₀=,x₁=-x₀,               ①

同理,x₂=-x₀,                                                              ②

由已知k₂=-λk₁,则x₂=-k₁-x₀.

设M(x_m,y_m),由,则

x_m=,把①②代入得x_m=-x₀,

即x_M+x₀=0,

∴线段PM中点在y轴上.

(3)解:∵P(1,-1)在抛物线y=ax²上,

∴a=-1,得抛物线y=-x².

由(2)的①式得x₁=-k₁-1.代入抛物线方程y=-x²得y₁=-(k₁+1)²,

将λ=1代入(2)的②式得x₂=k₁-1.

同理得y₂=-(k₁-1)²,

∴A(-k₁-1,-(k₁+1)²),B(k₁-1,-(k₁-1)²).

∴=(2k₁,4k₁),=(k₁+2,k₁²+2k₁).

∴·=2k₁(k₁+2)+4k₁(k₁²+2k₁)=2k₁(k₁+2)(2k₁+1).

∵∠PAB为钝角,

∴·＜0,

即k₁(k₁+2)(2k₁+1)＜0.

∴k₁＜-2或-＜k₁＜0.

又点A的纵坐标y₁=-(k₁+1)²,

当k₁＜-2时,y₁＜-1,

当-＜k₁＜0时,-1＜y₁＜-.

总之,点A的纵坐标的取值范围是(-∞,-1)∪(-1,-).