Question

6．如图，已知扇形AOP的半径为1，圆心角大小为$\frac{π}{3}$，等腰梯形ABCD是扇形AOP的内接梯形，顶点C，D分别在OP，OA上．顶点B在弧AP上，设∠AOB=θ．
（1）求出用θ表示等腰梯形ABCD的面积S的函数关系式；
（2）是否存在面积为$\frac{\sqrt{3}}{6}$的等腰梯形ABCD，若存在，求出此时梯形的高，若不存在，请说明理由．

Answer 1

分析 （1）利用已知条件，求出梯形的底边与高的长度，然后表示出梯形的面积．
（2）通过面积的值，求解正弦函数值，也就是梯形的高．推出结果即可．

解答 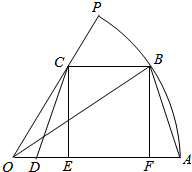解：（1）作BF⊥AD于F，CE⊥A于E，
则OF=cosθ，BF=sinθ，AF=1-cosθ，BC=OF-OE=cosθ-$\frac{sinθ}{tan\frac{π}{3}}$=cosθ-$\frac{\sqrt{3}}{3}sinθ$，
AD=BC+2AF=cosθ-$\frac{\sqrt{3}}{3}sinθ$+2（1-cosθ）=2-cosθ-$\frac{\sqrt{3}}{3}sinθ$，
S=$\frac{AD+CB}{2}×BF$=$\frac{（cosθ-\frac{\sqrt{3}}{3}sinθ+2-cosθ-\frac{\sqrt{3}}{3}sinθ）}{2}×sinθ$
=$（1-\frac{\sqrt{3}}{3}sinθ）sinθ$.$θ∈（0，\frac{π}{3}）$．
（2）存在面积为$\frac{\sqrt{3}}{6}$的等腰梯形ABCD，可得$（1-\frac{\sqrt{3}}{3}sinθ）sinθ=\frac{\sqrt{3}}{6}$，
可得-$\frac{\sqrt{3}}{3}{sin}^{2}θ+sinθ-\frac{\sqrt{3}}{6}=0$，
即：${2sin}^{2}θ-2\sqrt{3}sinθ+1=0$，
解得sin$θ=\sqrt{3}-1$，sinθ=$\sqrt{3}+1$（舍去）．
此时梯形的高：$\sqrt{3}-1$．

点评 本题考查函数的几何中的应用，三角函数的应用，三角方程的解法，考查计算能力．