
已知 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), 与
与 之间有关系|k
之间有关系|k +
+ |=
|= |
| -k
-k |,其中k>0,(Ⅰ)用k表示
|,其中k>0,(Ⅰ)用k表示 ;
;
(Ⅱ)求 ·
· 的最小值,并求此时
的最小值,并求此时 与
与 的夹角的大小。
的夹角的大小。
(Ⅰ) ·
·
 ;(Ⅱ)
;(Ⅱ) ·
· 的最小值为
的最小值为 ,
, 与
与 的夹角的大小60°.
的夹角的大小60°.
解析试题分析:(Ⅰ)用k表示 ,可由已知
,可由已知 ,
, ,可得
,可得 ,结合|k
,结合|k +
+ |=
|= |
| -k
-k |,像这种与向量的模有关,可采用两边平方法,这样两边平后可得
|,像这种与向量的模有关,可采用两边平方法,这样两边平后可得 ,整理后可用k表示
,整理后可用k表示 ,(Ⅱ)求
,(Ⅱ)求 ·
· 的最小值,由(Ⅰ)中函数的解析式,利用基本不等式,即可求出
的最小值,由(Ⅰ)中函数的解析式,利用基本不等式,即可求出 的最小值,利用最小值代入向量夹角公式,从而可得此时
的最小值,利用最小值代入向量夹角公式,从而可得此时 与
与 的夹角
的夹角 的大小.
的大小.
试题解析:(1)已知|ka+b|= |a-kb|,两边平方,得|ka+b|2=(
|a-kb|,两边平方,得|ka+b|2=( |a-kb|)2
|a-kb|)2
k2a2+b2+2ka·b=3(a2+k2b2-2ka·b)∴8k·a·b=(3-k2)a2+(3k2-1)b2
a·b = ∵a=(cosα,sinα),b=(cosβ,sinβ),
∵a=(cosα,sinα),b=(cosβ,sinβ),
∴a2="1," b2=1,∴a·b = =
=
(2)∵k2+1≥2k,即 ≥
≥ =
=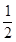 ∴a·b的最小值为
∴a·b的最小值为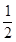 ,又∵a·b ="|" a|·|b |·cos
,又∵a·b ="|" a|·|b |·cos ,|a|=|b|=1∴
,|a|=|b|=1∴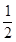 =1×1×cos
=1×1×cos 。∴
。∴ =60°,此时a与b的夹角为60°。
=60°,此时a与b的夹角为60°。
考点:平面向量的综合题.


科目:高中数学 来源: 题型:解答题
已知M(1+cos 2x,1),N(1, sin2x+a)(x∈R,a∈R,a是常数),且y=
sin2x+a)(x∈R,a∈R,a是常数),且y= ·
· (O为坐标原点).
(O为坐标原点).
(1)求y关于x的函数关系式y=f(x).
(2)若x∈[0, ]时,f(x)的最大值为2013,求a的值.
]时,f(x)的最大值为2013,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 ,其中向量
,其中向量 ,
, ,
, .在
.在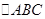 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,
, ,
, .
.
(1)如果三边 ,
, ,
, 依次成等比数列,试求角
依次成等比数列,试求角 的取值范围及此时函数
的取值范围及此时函数 的值域;
的值域;
(2) 在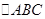 中,若
中,若 ,
,  ,求
,求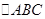 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且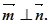
(Ⅰ)求 的大小;
的大小;
(Ⅱ)现给出下列四个条件:① ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 ,求出你所确定的
,求出你所确定的 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com