
(2010•西城区一模)已知圆C的参数方程为 (θ为参数),若P是圆C与y轴正半轴的交点,以原点为极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
(θ为参数),若P是圆C与y轴正半轴的交点,以原点为极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
在直角坐标系下,若矩阵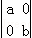 对应的变换将点P(2,﹣1)变到点p′(1,﹣2),则( )
对应的变换将点P(2,﹣1)变到点p′(1,﹣2),则( )
A.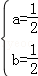 B.
B.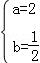 C.
C. D.
D.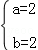
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
在同一平面直角坐标系中,直线x﹣2y=2变成直线2x′﹣y′=4的伸缩变换是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在同一坐标系中,将圆x2+y2=4在伸缩变换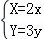 下的方程是( )
下的方程是( )
A.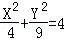 B.
B.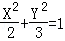 C.4X2+9Y2=1 D.2X2+3Y2=1
C.4X2+9Y2=1 D.2X2+3Y2=1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
(2011•温州二模)将函数y=﹣sinx(x∈[0,π])的图象绕原点顺时针方向旋转角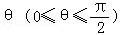 得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
A. B.
B.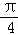 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
用与底面成45°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:选择题
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
A.1 B.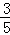 C.
C.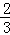 D.
D.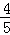
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
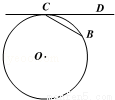
(2014•珠海二模)(几何证明选讲选做题)如图,CD是圆O的切线,切点为C,点B在圆O上,BC=2,∠BCD=30°,则圆O的面积为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:选择题
如图,PAB、PCD为⊙O的两条割线,AD、BC相交于点E,则图中相似三角形共有( )
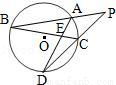
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com