
| A. | (-∞,1) | B. | (-∞,3) | C. | (-1,2) | D. | (-2,1) |
分析 根据题意,令g(x)=f(x)-2,则g(x)=f(x)-2=-2x5-x3-7x,分析可得g(x)的奇偶性与单调性,则f(a2)+f(a-2)>4,可以转化为g(a2)>-g(a-2),结合函数的奇偶性与单调性分析可得a2<2-a,解可得a的范围,即可得答案.
解答 解:根据题意,令g(x)=f(x)-2,
则g(x)=f(x)-2=-2x5-x3-7x,
g(-x)=-2(-x)5-(-x)3-7(-x)=-(-2x5-x3-7x),则g(x)为奇函数,
而g(x)=-2x5-x3-7x,则g′(x)=-10x4-2x2-7<0,则g(x)为减函数,
若f(a2)+f(a-2)>4,则有f(a2)-2>-[f(a-2)-2],
即g(a2)>-g(a-2),
即g(a2)>g(2-a),
则有a2<2-a,
解可得-2<a<1,
即a的取值范围是(-2,1);
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是构造函数,进而分析该函数的奇偶性、单调性.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
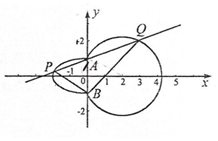 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com