
分析 (1)利用三种方程的转化方法,求曲线C1普通方程和C2的直角坐标方程;
(2)C2的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=-1+tsinα}\end{array}\right.$(t为参数),代入$\frac{{x}^{2}}{4}+{y}^{2}$=1,得$(\frac{1}{4}co{s}^{2}α+si{n}^{2}α){t}^{2}$-2tsinα=0,利用参数的意义,求|AB|的最大值及此时点B的坐标.
解答 解:(1)曲线C1的参数方程为$\left\{\begin{array}{l}{x=2cosφ}\\{y=sinφ}\end{array}\right.$(其中φ为参数),
普通方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;曲线C2的极坐标方程为ρ(tanα•cosθ-sinθ)=1,
直角坐标方程为xtanα-y-1=0;
(2)C2的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=-1+tsinα}\end{array}\right.$(t为参数),
代入$\frac{{x}^{2}}{4}+{y}^{2}$=1,得$(\frac{1}{4}co{s}^{2}α+si{n}^{2}α){t}^{2}$-2tsinα=0,
∴t1+t2=$\frac{2sinα}{\frac{1}{4}co{s}^{2}α+si{n}^{2}α}$,t1t2=0,
∴|AB|=|$\frac{2sinα}{\frac{1}{4}co{s}^{2}α+si{n}^{2}α}$|=|$\frac{8}{3sinα+\frac{1}{sinα}}$|,
∵0<α<π,且α≠$\frac{π}{2}$,
∴sinα∈(0,1),
∴|AB|max=$\frac{4\sqrt{3}}{3}$,此时B的坐标为($±\frac{4\sqrt{2}}{3}$,$\frac{1}{3}$).
点评 本题考查三种方程的转化,考查参数方程的运用,属于中档题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | a≤-4 | B. | -4≤a≤6 | C. | a≤-4或a≥6 | D. | a≥6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
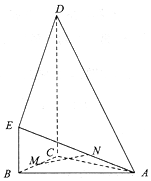 如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.
如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{7},1})$ | B. | $({\frac{1}{3},3})$ | C. | $({\frac{1}{2},2})$ | D. | $({2,\frac{7}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (-1,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 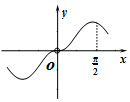 | C. | 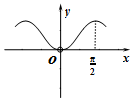 | D. | 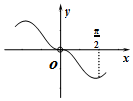 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 648个 | B. | 720个 | C. | 900个 | D. | 1000个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com