
| A. |  | B. | 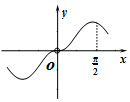 | C. | 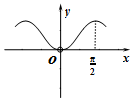 | D. | 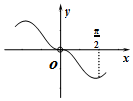 |
分析 判断函数的奇偶性,排除选项,求出函数的导数,利用函数的单调性排除选项,推出结果.
解答 解:因为函数$y=f(x)=\frac{2sinx}{{1+\frac{1}{x^2}}}$可化简为$f(x)=\frac{{2{x^2}sinx}}{{{x^2}+1}}$可知函数为奇函数关于原点对称,可排除答案C;
同时有$y'=f'(x)=\frac{{4xsinx+2{x^4}cosx+2{x^2}cosx}}{{{{({x^2}+1)}^2}}}$=$\frac{{2x(2sinx+{x^3}cosx+xcosx)}}{{{{({x^2}+1)}^2}}}$,
故函数在$x∈(0,\frac{π}{2})$时f'(x)>0,则$x∈(0,\frac{π}{2})$上单调递增,排除答案B和D,
故选:A.
点评 本题考查函数的图象的判断与应用,函数的导数判断函数的单调性,考查计算能力.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
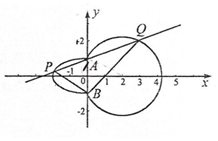 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
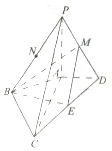 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com