
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出函数的导数,表示出截距b=ea(-a3+a),记g(a)=ea(-a3+a),根据函数的单调性求出截距的范围即可.
解答 解:(Ⅰ)f'(x)=ex(x2-2x+a)+ex(2x-2)=ex(x2+a-2),
当a≥2时,f'(x)≥0恒成立,函数f(x)的递增区间是R;
当a<2时,$f'(x)≥0?{x^2}≥2-a?x≤-\sqrt{2-a}$或$x≥\sqrt{2-a}$,
函数f(x)的递增区间是$(-∞,-\sqrt{2-a}),(\sqrt{2-a},+∞)$,递减区间是$(-\sqrt{2-a},\sqrt{2-a})$;
(Ⅱ)f(a)=ea(a2-a),f'(a)=ea(a2+a-2),
所以直线l的方程为:y-ea(a2-a)=ea(a2+a-2)(x-a),令x=0得到:
截距b=ea(-a3+a),记g(a)=ea(-a3+a),g'(a)=ea(-a3-3a2+a+1),
记h(a)=-a3-3a2+a+1⇒h'(a)=-3a2-6a+1<0(∵1≤a≤3)
所以h(a)递减,h(a)≤h(1)=-2<0,
∴g'(a)<0,即g(a)在区间[1,3]上单调递减,
∴g(3)≤g(a)≤g(1),即截距的取值范围是:[-24e3,0].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
| 古文迷 | 非古文迷 | 合计 | |
| 男生 | 26 | 24 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{7},1})$ | B. | $({\frac{1}{3},3})$ | C. | $({\frac{1}{2},2})$ | D. | $({2,\frac{7}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 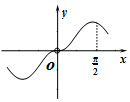 | C. | 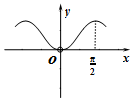 | D. | 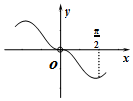 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 648个 | B. | 720个 | C. | 900个 | D. | 1000个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com