
分析 (1)求出a=3时,f(x)的解析式,去掉绝对值,运用二次不等式的解法,即可得到所求解集;
(2)由题意可得|x2-2x+a-1|-a2-2a≥0对x∈R恒成立,即有|(x-1)2+a-2|-a2-2a≥0对x∈R恒成立.再讨论a-2≤0和a-2>0,可得a的不等式,解不等式求交集,即可得到所求a的范围.
解答 解:(1)当a=3时,f(x)=|x2-2x+2|-15,
由x2-2x+2>0恒成立,则f(x)=x2-2x-13,
由f(x)≥-10,可得x2-2x-3≥0,
解得x≥3或x≤-1,
即f(x)≥-10的解集为{x|x≥3或x≤-1};
(2)f(x)≥0对x∈R恒成立,
即为|x2-2x+a-1|-a2-2a≥0对x∈R恒成立,
即有|(x-1)2+a-2|-a2-2a≥0对x∈R恒成立.
当a-2≤0即a≤2时,只需a2+2a≤0,即-2≤a≤0;
当a-2>0,即a>2时,只需a2+2a≤a-2,即a2+a+2≤0,
由判别式△=1-4×2<0,可得不等式无实数解.
综上可得,a的取值范围是[-2,0].
点评 本题考查含绝对值的不等式的解法,不等式恒成立问题的解法,考查绝对值的含义和配方法、分类讨论的思想方法,以及运算求解能力,属于中档题.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{12}$个单位长度 | B. | 向右平行移动$\frac{π}{12}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
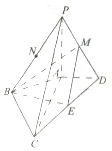 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | 2π | C. | π2 | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题¬p是真命题 | |
| B. | 命题p是特称命题 | |
| C. | 命题p是全称命题 | |
| D. | 命题p既不是全称命题也不是特称命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com