
分析 (1)利用|$\overrightarrow{BP}$|=|$\overrightarrow{AC}$|,由|$\overrightarrow{AP}$|+|$\overrightarrow{AC}$|=4,得,|$\overrightarrow{AP}$|+|$\overrightarrow{BP}$|=4,即可求P的轨迹E;
(2)所以由韦达定理:k1+k2=$\frac{2{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-3}$,k1k2=$\frac{{{y}_{0}}^{2}-3}{{{x}_{0}}^{2}-3}$,两式相除:$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{2{x}_{0}{y}_{0}}{{{y}_{0}}^{2}-3}$,即可得出结论.
解答 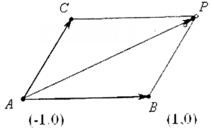 解:(1)如图因为$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$,所以四边形ACPB是平行四边形,
解:(1)如图因为$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$,所以四边形ACPB是平行四边形,
所以|$\overrightarrow{BP}$|=|$\overrightarrow{AC}$|,
由|$\overrightarrow{AP}$|+|$\overrightarrow{AC}$|=4,得,|$\overrightarrow{AP}$|+|$\overrightarrow{BP}$|=4,
所以P的轨迹是以A,B为焦点的椭圆,a=2,c=1,b=$\sqrt{3}$,
所以方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(2)设P(x0,y0),过P的斜率为k的直线为y-y0=k(x-x0),
由直线与圆O相切可得$\frac{|y-k{x}_{0}|}{\sqrt{{k}^{2}+1}}$=$\sqrt{3}$,即:$({{x}_{0}}^{2}-3){k}^{2}-2{x}_{0}{y}_{0}k+{{y}_{0}}^{2}-3=0$,
由已知可知k1,k2是方程$({{x}_{0}}^{2}-3){k}^{2}-2{x}_{0}{y}_{0}k+{{y}_{0}}^{2}-3=0$的两个根,
所以由韦达定理:k1+k2=$\frac{2{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-3}$,k1k2=$\frac{{{y}_{0}}^{2}-3}{{{x}_{0}}^{2}-3}$,
两式相除:$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{2{x}_{0}{y}_{0}}{{{y}_{0}}^{2}-3}$,
又因为${{y}_{0}}^{2}-3$=-$\frac{3}{4}{{x}_{0}}^{2}$,
代入上式可得,$\frac{1}{{k}_{0}}$($\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$)=-$\frac{8}{3}$为一个定值.
点评 本题考查向量知识的运用,考查椭圆的定义,考查直线与圆位置关系的运用,考查韦达定理,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | B. | ?x≤1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | C. | ?x0>1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ | D. | ?x0≤1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<3} | B. | {x|x≤-2} | C. | {x|x<-2} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{2}$] | B. | (-∞,-1]∪[$\frac{1}{2}$,+∞) | C. | [0,$\frac{4}{3}$] | D. | (-∞,-2]∪[$\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
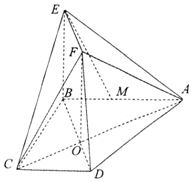 如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.
如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | 2π | C. | π2 | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com