
| A. | ?x>1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | B. | ?x≤1,${(\frac{1}{2})^x}≥\frac{1}{2}$ | C. | ?x0>1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ | D. | ?x0≤1,${(\frac{1}{2})^{x_0}}≥\frac{1}{2}$ |
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:解答题
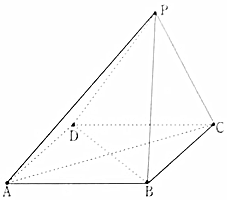 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,且有PB=PD,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6和2.4 | B. | 4和5.6 | C. | 4和2.4 | D. | 6和5.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$或$\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{3}$或$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com