练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知随机变量X+Y=10，若X～B（10，0.6），则E（Y），D（Y）分别是（　　）
    A．6和2.4B．4和5.6C．4和2.4D．6和5.6

    分析 先由X～B（10，0.6），得均值E（X）=6，方差D（X）=2.4，然后由X+Y=10得Y=-X+10，再根据公式求解即可．

    解答 解：由题意X～B（10，0.6），知随机变量X服从二项分布，n=10，p=0.6，
    则均值E（X）=np=6，方差D（X）=npq=2.4，
    又∵X+Y=10，
    ∴Y=-X+10，
    ∴E（Y）=-E（X）+10=-6+10=4，
    D（Y）=D（X）=2.4．
    故选：C．

    点评 解题关键是若两个随机变量Y，X满足一次关系式Y=aX+b（a，b为常数），当已知E（X）、D（X）时，则有E（Y）=aE（X）+b，D（Y）=a2D（X）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知$cos（{α-\frac{π}{3}}）=-\frac{1}{2}$，则$sin（{\frac{π}{6}+α}）$的值等于（　　）
    A．$\frac{\sqrt{3}}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{1}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设f（x）=|x-b|+|x+b|．
    （1）当b=1时，求f（x）≤x+2的解集；
    （2）当x=1时，若不等式f（x）≥$\frac{|a+1|-|2a-1|}{|a|}$对任意实数a≠0恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知点A，B的坐标分别为（-$\sqrt{2}$，0），（$\sqrt{2}$，0），直线AM，BM相交于点M，且它们的斜率之积是-$\frac{1}{2}$，点M的轨迹为曲线E．
    （Ⅰ）求E的方程；
    （Ⅱ）过点F（1，0）作直线l交曲线E于P，Q两点，交y轴于R点，若$\overrightarrow{RP}$=λ1$\overrightarrow{PF}$，$\overrightarrow{RQ}$=λ2$\overrightarrow{QF}$，求证：λ1+λ2为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设函数f（x）=（x-a）（x-b）（x-c）（其中a＞1，b＞1），x=0是f（x）的一个零点，曲线y=f（x）在点（1，f（1））处的切线平行于x轴，则a+b的最小值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示：

    （1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
    （2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案：
    ①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
    ②每次赠送的随机话费和对应概率如下：
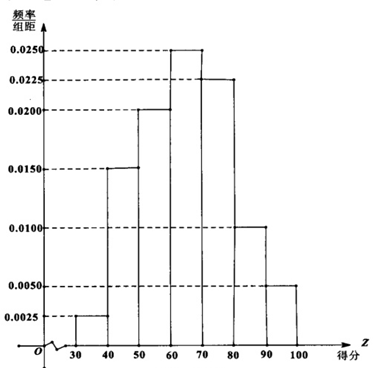
    赠送话费（单位：元）1020
    概率$\frac{2}{3}$ $\frac{1}{3}$ 
    现有一位市民要参加此次问卷调查，记X（单位：元）为该市民参加问卷调查获赠的话费，求X的分布列．
    附：$\sqrt{210}$≈14.5
    若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右顶点为A（2，0），左、右焦点分别为F1、F2，过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P，与椭圆交于另一个点B，且点B在x轴上的射影恰好为点F1．
    （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）过点P且斜率大于$\frac{1}{2}$的直线与椭圆交于M，N两点（|PM|＞|PN|），若S△PAM：S△PBN=λ，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．命题“?x＞1，${（\frac{1}{2}）^x}＜\frac{1}{2}$”的否定是（　　）
    A．?x＞1，${（\frac{1}{2}）^x}≥\frac{1}{2}$B．?x≤1，${（\frac{1}{2}）^x}≥\frac{1}{2}$C．?x0＞1，${（\frac{1}{2}）^{x_0}}≥\frac{1}{2}$D．?x0≤1，${（\frac{1}{2}）^{x_0}}≥\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

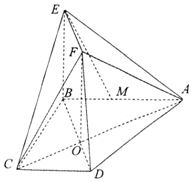    16．如图所示，直角梯形ABCD两条对角线AC，BD的交点为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，M为线段AB上一点，AM=2MB，且AB⊥BC，AB∥CD，AB=BE=6，CD=BC=3．
    （I）求证：EM∥平面ADF；
    （Ⅱ）求二面角O-EF-C的余弦值．

    查看答案和解析>>

    同步练习册答案