
分析 由题意可得f(0)=0,即c=0,求出f(x)的导数,运用导数的几何意义,可得3+ab=2(a+b),运用基本不等式即可得到所求最小值.
解答 解:函数f(x)=(x-a)(x-b)(x-c)(其中a>1,b>1),x=0是f(x)的一个零点,
可得f(0)=0,即-abc=0,可得c=0,
即f(x)=x(x-a)(x-b)=x3-(a+b)x2+abx,
f′(x)=3x2-2(a+b)x+ab,
由曲线y=f(x)在点(1,f(1))处的切线平行于x轴,
可得3-2(a+b)+ab=0,
即3+ab=2(a+b),
由a>1,b>1,可得ab≤($\frac{a+b}{2}$)2,
当且仅当a=b取得等号,
即有2(a+b)≤3+($\frac{a+b}{2}$)2,
解得a+b≥6或a+b≤2(舍去),
则当且仅当a=b=3时,取得最小值6.
故答案为:6.
点评 本题考查函数的零点的概念的运用和导数的运用:求切线的斜率,考查基本不等式的运用:求最值,以及运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 古文迷 | 非古文迷 | 合计 | |
| 男生 | 26 | 24 | 50 |
| 女生 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
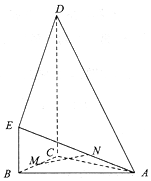 如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.
如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6和2.4 | B. | 4和5.6 | C. | 4和2.4 | D. | 6和5.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{7},1})$ | B. | $({\frac{1}{3},3})$ | C. | $({\frac{1}{2},2})$ | D. | $({2,\frac{7}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com