Question

3．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），过双曲线右焦点F倾斜角为$\frac{π}{4}$的直线与该双曲线的渐近线分别交于M、N．若|FM|=2|FN|，则该双曲线的离心率等于（　　）

• A． $\frac{\sqrt{10}}{3}$
• B． $\sqrt{3}$
• C． $\sqrt{3}$或$\frac{\sqrt{10}}{3}$
• D． $\frac{\sqrt{10}}{3}$或$\sqrt{10}$

Answer 1

分析 求出双曲线的渐近线方程，讨论b＞a＞0，可得N为FM的中点．当a＞b＞0时，可得$\overrightarrow{FM}$=-2$\overrightarrow{FN}$，求出直线MN的方程，联立渐近线方程可得M，N的坐标，求得b=3a或a=3b，再由离心率公式即可得到所求值．

解答 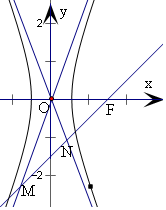解：双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x，
当b＞a＞0时，如右图．
若|FM|=2|FN|，可得N为FM的中点．
由直线MN：y=x-c，联立y=$\frac{b}{a}$x，可得M（$\frac{ac}{a-b}$，$\frac{bc}{a-b}$），
由直线MN：y=x-c，联立y=-$\frac{b}{a}$x，可得N（$\frac{ac}{a+b}$，-$\frac{bc}{a+b}$），
由F（c，0），可得-$\frac{2bc}{a+b}$=$\frac{bc}{a-b}$，
化简为b=3a，
即有e=$\frac{c}{a}$=$\sqrt{1+（\frac{b}{a}）^{2}}$=$\sqrt{1+9}$=$\sqrt{10}$；
当a＞b＞0时，如右图．
若|FM|=2|FN|，可得$\overrightarrow{FM}$=-2$\overrightarrow{FN}$，
由直线MN：y=x-c，联立y=$\frac{b}{a}$x，可得M（$\frac{ac}{a-b}$，$\frac{bc}{a-b}$），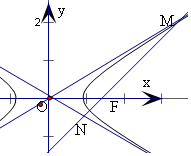
由直线MN：y=x-c，联立y=-$\frac{b}{a}$x，可得N（$\frac{ac}{a+b}$，-$\frac{bc}{a+b}$），
由F（c，0），可得$\frac{bc}{a-b}$=-2•（-$\frac{bc}{a+b}$），
化简为a=3b，
即有e=$\frac{c}{a}$=$\sqrt{1+（\frac{b}{a}）^{2}}$=$\sqrt{1+\frac{1}{9}}$=$\frac{\sqrt{10}}{3}$．
则该双曲线的离心率等于$\frac{\sqrt{10}}{3}$或$\sqrt{10}$．
故选：D．

点评 本题考查双曲线的离心率的求法，注意运用双曲线的渐近线方程，以及分类讨论的思想方法，以及向量共线的坐标表示，考查运算能力，属于中档题．