
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() 为线段
为线段![]() 上一点,
上一点,![]() 为
为![]() 的中点.
的中点.
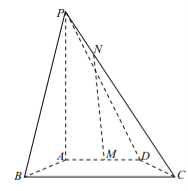
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连
,连![]() ,然后利用中位线定理结合已知条件证明得
,然后利用中位线定理结合已知条件证明得![]() 是平行四边形,从而利用平行四边形的性质可使问题得证;(2)根据已知条件结合线面垂直的性质定理推出
是平行四边形,从而利用平行四边形的性质可使问题得证;(2)根据已知条件结合线面垂直的性质定理推出![]() 平面
平面![]() ,由此可求得
,由此可求得![]() 点到平面
点到平面![]() 的距离.
的距离.
试题解析:(1)过N作NE∥BC,交PB于点E,连AE,
∵CN=3NP,∴EN∥BC且EN=BC,
又∵AD∥BC,BC=2AD=4,M为AD的中点,
∴AM∥BC且AM=BC,∴EN∥AM且EN=AM,
∴四边形AMNE是平行四边形,∴MN∥AE,
又∵MN平面PAB,AE平面PAB,∴MN∥平面PAB. …6分
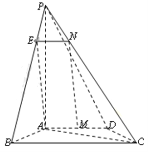
(2)连接AC,在梯形ABCD中,
由BC=2AD=4,AB=CD,∠ABC=60°,得AB=2,∴AC=2,AC⊥AB.
∵PA⊥平面ABCD,∴PA⊥AC.
又∵PA∩AB=A,∴AC⊥平面PAB.
又∵CN=3NP,∴N点到平面PAB的距离d=AC=. …12分


科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E,F在圆O上,且AB//EF,AB=2EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.
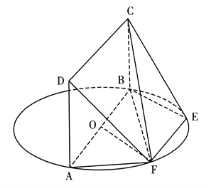
(I)证明:OF//平面BEC;
(Ⅱ)证明:平面ADF![]() 平面BCF.
平面BCF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数,给出下列命题:
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 017,则f(x)是周期函数;
③若函数g(x)=![]() 是偶函数,则f(x)=x+1;
是偶函数,则f(x)=x+1;
④函数y=![]() 的定义域为
的定义域为![]() .
.
其中正确的命题是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程: ![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据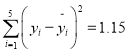 )
)
参考公式:相关指数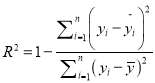
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 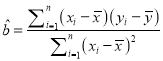 ,
, ![]() .参考数据:
.参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的方程为
的方程为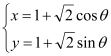 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(II)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品每件进价9元,售价20元,每天可卖出69件.若售价降低,销售量可以增加,且售价降低![]() 元时,每天多卖出的件数与
元时,每天多卖出的件数与![]() 成正比.已知商品售价降低3元时,一天可多卖出36件.
成正比.已知商品售价降低3元时,一天可多卖出36件.
(Ⅰ)试将该商品一天的销售利润表示成![]() 的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.
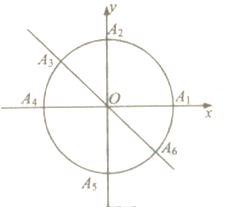
(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com