Question

由数字1、2、3、4、5、6组成无重复数字的数中，求：
（1）六位偶数的个数；
（2）求三个偶数互不相邻的六位数的个数；
（3）求恰有两个偶数相邻的六位数的个数；
（4）奇数字从左到右，从小到大依次排列的六位数的个数．

Answer 1

（1）360,（2）144,（3）432,（4）120.

解析试题分析：（1）根据排列组合中特殊元素、特殊位置优先考虑的原则，先考虑个位数. 偶数的个位数字必须是偶数,有3种选择，剩下5个元素进行全排列，有种排法，根据分步计数原理得满足条件的六位偶数共有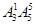=360个，（2）不相邻问题用插空法解决，先排奇数，有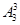种排法，产生4个空，从四个空选三，排偶数，有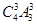，根据分步计数原理得满足条件的三个偶数互不相邻的六位数有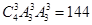个，（3）相邻问题用捆绑法解决，先从三个偶数中选出两个捆绑在一起看作一个偶数，有种选法，因为与第三个偶数不相邻，因此进行不相邻排列：先排奇数再从四个空里选两个空插这两个元素，根据分步计数原理得满足条件的恰有两个偶数相邻的六位数共有=432个，不要忘记两个捆绑的偶数也要全排列.（4）有序排列，只需选不需排，即从6个位置中选3个填奇数，再排偶数，即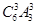=120个.或用除法，除去顺序数，即=120个.
（1）偶数的个位数字必须是偶数。因而先排个位
满足条件的六位偶数共有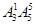=360个；             3分
（2）先排奇数，然后有三个空，再插空排三个偶数
满足条件的三个偶数互不相邻的六位数有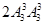=72个；               6分
（3）用捆绑法。先从三个偶数中选出两个捆绑在一起看作一个偶数，然后排奇数，
再从四个空里选两个空插这两个元素。满足条件的恰有两个偶数相邻的六位
数共有=432个；         10分
（4）满足条件的奇数字从左到右从小到大依次排列的六位数共有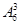=120个     15分
考点：排列组合