练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知在的展开式中，第6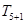项为常数项.
    （1）求n；
    （2）问展开式中的有理项.分别为第几项？说明理由。

    （1）；（2）展开式中的有理项分别为第项，理由详见试题解析.

    解析试题分析：（1）用二项式定理的展开项即可求n的值；
    （2）令展开式中的指数为整数的项即为有理项，求出的值即可.
    （1）  
      故.      
    （2）设展开式中的有理项为  
    则，故r =2，5，8 
    展开式中的有理项分别为第3项，第6项，第9项.
    考点：二项式定理.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （14分）已知在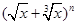（其中n<15）的展开式中：
    （1）求二项式展开式中各项系数之和；
    （2）若展开式中第9项，第10项，第11项的二项式系数成等差数列，求n的值；
    （3）在（2）的条件下写出它展开式中的有理项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    由数字1、2、3、4、5、6组成无重复数字的数中，求：
    （1）六位偶数的个数；
    （2）求三个偶数互不相邻的六位数的个数；
    （3）求恰有两个偶数相邻的六位数的个数；
    （4）奇数字从左到右，从小到大依次排列的六位数的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （10分）盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同.
    （1）从盒中一次随机抽出2个球，求取出的2个球的颜色相同的概率；
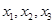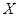    （2）从盒中一次随机抽出4个球，其中红球、黄球、绿球的个数分别为，随机变量表示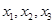的最大数，求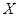的概率分布和数学期望.

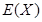    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （2013•浙江）设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．
    （1）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和．，求ξ分布列；
    （2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若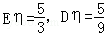，求a：b：c．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知n展开式中的二项式系数的和比(3a＋2b)7展开式的二项式系数的和大128，求n展开式中的系数最大的项和系数最小的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图所示，在以AB为直径的半圆周上，有异于A，B的六个点C1，C2，…，C6，直径AB上有异于A，B的四个点D1，D2，D3，D4.则：

    (1)以这12个点(包括A，B)中的4个点为顶点，可作出多少个四边形？
    (2)以这10个点(不包括A，B)中的3个点为顶点，可作出多少个三角形？其中含点C1的有多少个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知+++…+=（nεN）
    （I）求n的值
    （II）求二项式  的一次项

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    展开式中的系数是               。

    查看答案和解析>>

    同步练习册答案