
(10分)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机抽出2个球,求取出的2个球的颜色相同的概率;
(2)从盒中一次随机抽出4个球,其中红球、黄球、绿球的个数分别为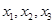 ,随机变量
,随机变量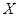 表示
表示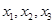 的最大数,求
的最大数,求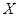 的概率分布和数学期望
的概率分布和数学期望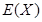 .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
某研究性学习小组有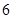 名同学.
名同学.
(1)这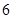 名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
(2)从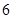 名同学中选
名同学中选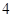 人参加班级
人参加班级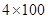 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com