
某研究性学习小组有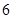 名同学.
名同学.
(1)这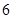 名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
(2)从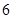 名同学中选
名同学中选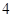 人参加班级
人参加班级 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种?
(1)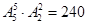 ;(2)
;(2)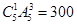 .
.
解析试题分析:(1)对于相邻问题采用捆绑后,将甲乙捆绑后当成一个人与其他四人一起排列,最后根据分步计数原理即可得到甲乙相邻有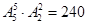 种排法;(2)方法一,先按丙同学有没有参加接力进行分类,进而求出这两种情况下的方法数,最后将这两类的方法数相加即可;法二,分两步走,第一步先确定第一棒是由除丙以外的哪个同学跑,第二步确定第二、三、四棒是由哪几位同学去跑,进而根据分步计数原理即可得到满足要求的方法数
种排法;(2)方法一,先按丙同学有没有参加接力进行分类,进而求出这两种情况下的方法数,最后将这两类的方法数相加即可;法二,分两步走,第一步先确定第一棒是由除丙以外的哪个同学跑,第二步确定第二、三、四棒是由哪几位同学去跑,进而根据分步计数原理即可得到满足要求的方法数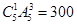 .
.
(1)分两步走:第一步先将甲乙捆绑有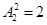 种方法;第二步,甲乙两人捆绑后与其他四人一起排列有
种方法;第二步,甲乙两人捆绑后与其他四人一起排列有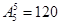 种方法,所以这
种方法,所以这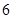 名同学排成一排照相,则同学甲与同学乙相邻的排法有
名同学排成一排照相,则同学甲与同学乙相邻的排法有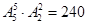 种;
种;
(2)法一:分成两类:第一类,同学丙没有参加接力比赛的安排方法有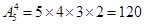 种;第二类,同学两参加接力比赛但不跑第一棒的安排方法有
种;第二类,同学两参加接力比赛但不跑第一棒的安排方法有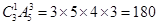 ;综上可知从
;综上可知从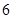 名同学中选
名同学中选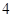 人参加班级
人参加班级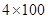 接力比赛,则同学丙不跑第一棒的安排方法有
接力比赛,则同学丙不跑第一棒的安排方法有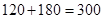 种;
种;
法二:跑第一棒的选法有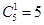 种方法;第二、三、四棒的选法有
种方法;第二、三、四棒的选法有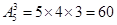 种方法,所以从
种方法,所以从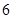 名同学中选
名同学中选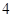 人参加班级
人参加班级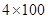 接力比赛,则同学丙不跑第一棒的安排方法有
接力比赛,则同学丙不跑第一棒的安排方法有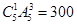 种.
种.
考点:1.两个计数原理;2.排列问题.


科目:高中数学 来源: 题型:解答题
设有5幅不同的国画,2幅不同的油画,7幅不同的水彩画.
(1)从这些国画、油画、水彩画中各选一幅画布置房间,有几种不同的选法?
(2)从这些画中任选出两幅不同画种的画布置房间,有几种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
7个人排成一排,按下列要求各有多少种排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知(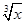 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-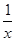 )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机抽出2个球,求取出的2个球的颜色相同的概率;
(2)从盒中一次随机抽出4个球,其中红球、黄球、绿球的个数分别为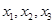 ,随机变量
,随机变量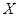 表示
表示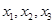 的最大数,求
的最大数,求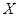 的概率分布和数学期望
的概率分布和数学期望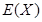 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设m,n∈N*,f(x)=(1+2x)m+(1+x)n.
(1)当m=n=2 011时,记f(x)=a0+a1x+a2x2+…+a2 011x2 011,求a0-a1+a2-…-a2 011;
(2)若f(x)展开式中x的系数是20,则当m,n变化时,试求x2系数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com