
有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有多少种?
1 248(种)
解析解:由题意知中间行的两张卡片的数字之和是5,因此中间行的两个数字应是1,4或2,3.若中间行两个数字是1,4,则有A22种排法,此时A、B、E、F的数字有以下几类:
(1)若不含2,3,共有A44=24(种)排法.A B C D E F
(2)若含有2,3中的一个,则有C21C43A44=192(种)(C21是从2,3中选一个,C43是从5,6,7,8中选3个,A44将选出的4个数字排在A、B、E、F处).
(3)含有2,3中的两个,此时2,3不能排在一行上,因此可先从2,3中选1个,排在A,B中一处,有C21A21种,剩下的一个排在E、F中的一处有A21种,然后从5,6,7,8中选2个排在剩余的2个位置有A42种.
因此共有C21A21A21A42=96(种)排法.
所以中间一行数字是1,4时共有A22(24+192+96)=624(种).当中间一行数字是2,3时也有624种.因此满足要求的排法共有624×2=1 248(种).


科目:高中数学 来源: 题型:解答题
某研究性学习小组有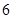 名同学.
名同学.
(1)这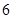 名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?
(2)从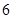 名同学中选
名同学中选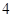 人参加班级
人参加班级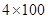 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在(3-x)20(x∈R,x≠0)的展开式中,已知第2r项与第r+1项(r≠1)的二项式系数相等.
(1)求r的值;
(2)若该展开式的第r项的值与倒数第r项的值的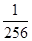 相等,求x的值.
相等,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班一天上午有4节课,每节都需要安排一名教师去上课,现从A,B,C,D,E,F,6名教师中安排4人分别上一节课,第一节课只能从A、B两人中安排一人,第四节课只能从A、C两人中安排一人,则不同的安排方案共有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com