
已知二项式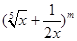 的展开式中第2项为常数项
的展开式中第2项为常数项 ,其中
,其中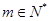 ,且展开式按
,且展开式按 的降幂排列.
的降幂排列.
(1)求 及
及 的值.
的值.
(2)数列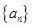 中,
中, ,
,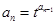 ,
,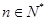 ,求证:
,求证: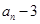 能被4整除.
能被4整除.
(1)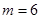 ,
,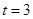 ;(2))证明过程详见解析.
;(2))证明过程详见解析.
解析试题分析:(1)由展开式中第2项为常数项,则可根据二项式展开式的第2项展开式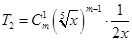 中未知数
中未知数 的指数为0,从而求出
的指数为0,从而求出 的值,将
的值,将 的值代回第2项展式可求出
的值代回第2项展式可求出 的值;(2)可利用数学归纳法来证明,①当
的值;(2)可利用数学归纳法来证明,①当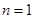 时,
时,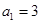 ,
,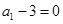 ,能被4整除,显然命题成立;②假设当n=k时,
,能被4整除,显然命题成立;②假设当n=k时,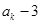 能被4整除,即
能被4整除,即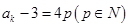 .那么当n =k+1时,
.那么当n =k+1时,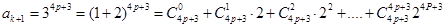
=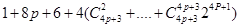 =
=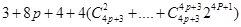
=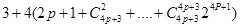 显然
显然 是非负整数,
是非负整数,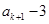 能被4整除.
能被4整除.
由①、②可知,命题对一切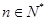 都成立.
都成立.
试题解析:(1) 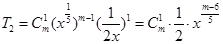 , 2分
, 2分
故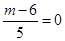 ,
,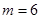 ,
,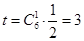 . 4分
. 4分
(2)证明:①当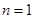 时,
时,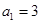 ,
,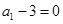 ,能被4整除.
,能被4整除.
②假设当n=k时,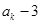 能被4整除,即
能被4整除,即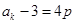 ,其中p是非负整数.
,其中p是非负整数.
那么当n =k+1时,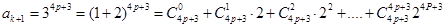
=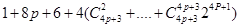 =
=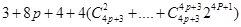
=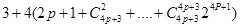 显然
显然 是非负整数,
是非负整数,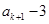 能被4整除.
能被4整除.
由①、②可知,命题对一切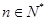 都成立. 10分
都成立. 10分
考点:1.二项式定理;2.数学归纳法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知(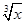 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-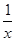 )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在产品质量检验时,常从产品中抽出一部分进行检查.现在从98件正品和2件次品共100件产品中,任意抽出3件检查.
(1)共有多少种不同的抽法?
(2)恰好有一件是次品的抽法有多少种?
(3)至少有一件是次品的抽法有多少种?
(4)恰好有一件是次品,再把抽出的3件产品放在展台上,排成一排进行对比展览,共有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从5名女同学和4名男同学中选出4人参加演讲比赛,分别按下列要求,各有多少种不同的选法?
(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)在(2)的前提下,男同学甲与女同学乙不能同时选出.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知甲、乙、丙等6人 .
(1)这6人同时参加一项活动,必须有人去,去几人自行决定,共有多少种不同的去法?
(2)这6人同时参加6项不同的活动,每项活动限1人参加,其中甲不参加第一项活动,乙不参加第三项活动,共有多少种不同的安排方法?
(3)这6人同时参加4项不同的活动,求每项活动至少有1人参加的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com