
一次函数 是
是 上的增函数,
上的增函数, ,已知
,已知 .
.
(1)求 ;
;
(2)若 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(3)当 时,
时, 有最大值
有最大值 ,求实数
,求实数 的值.
的值.
(1)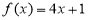 ;(2)
;(2)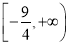 ;(3)
;(3) 或
或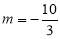 .
.
【解析】
试题分析:(1)先设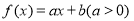 ,然后由
,然后由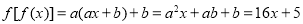 恒成立得方程组
恒成立得方程组 ,求解方程组即可,注意取
,求解方程组即可,注意取 的解;(2)由(1)得
的解;(2)由(1)得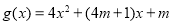 ,根据二次函数的图像与性质可知,要使
,根据二次函数的图像与性质可知,要使 在
在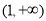 单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.
单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.
试题解析:(1)∵ 是
是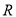 上的增函数,∴设
上的增函数,∴设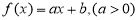 1分
1分

∴ 3分
3分
解得 或
或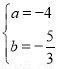 (不合题意舍去) 5分
(不合题意舍去) 5分
∴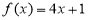 6分
6分
(2)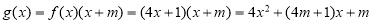 7分
7分
对称轴 ,根据题意可得
,根据题意可得 8分
8分
解得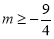
∴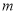 的取值范围为
的取值范围为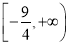 9分
9分
(3)①当 时,即
时,即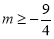 时
时
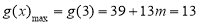 ,解得
,解得 ,符合题意 11分
,符合题意 11分
②当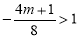 时,即
时,即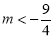 时
时
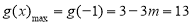 ,解得
,解得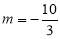 ,符合题意 13分
,符合题意 13分
由①②可得 或
或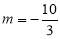 14分.
14分.
考点:1.函数的解析式;2.二次函数的图像与性质;3.函数的单调性与最值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016届广东实验中学高一一级模块考试数学试卷(解析版) 题型:选择题
如图将正方形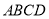 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论:

① ⊥
⊥ ;
;
②△ 是等边三角形;
是等边三角形;
③ 与
与 所成的角为60°;
所成的角为60°;
④ 与平面
与平面 所成的角为60°.
所成的角为60°.
其中错误的结论是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一年级月考(三)数学试卷(解析版) 题型:选择题
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中能较好地反映计算机在第 天被感染的数量
天被感染的数量 与
与 之间的关系的是 ( )
之间的关系的是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届山东枣庄第三中学高一第一学期期末考试数学试卷(解析版) 题型:解答题
已知直线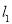 :
: ,(
,( 不同时为0),
不同时为0),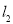 :
: ,
,
(1)若 且
且 ,求实数
,求实数 的值;
的值;
(2)当 且
且 时,求直线
时,求直线 与
与 之间的距离
之间的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com