解:(1)∵log
ab•log
ba=1
∴log
ab=

又∵a>b>1,
∴log
ba>1
由log
ab+log
ba=

得log
ba+

=

解得:log
ba=3
∴log
ab=

=

∴log
ab-log
ba=-

(2)若a=0,则y=-3x+3,在函数在区间[1,3]的最小值为-6,不符合条件.
若a<0,则函数y=ax
2-3x+3图象的开口方向朝下,且对称轴x=
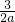
<0,
此时函数y=ax
2-3x+3在区间[1,3]的最大值小于3,故其最小值不可能是8,不符合条件
若a>0,则函数y=ax
2-3x+3图象的开口方向朝上,且对称轴x=
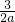
>0,
当
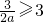
,即
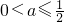
时,y的最小值在x=3处取到,最小值为9a-6,令9a-6=8,得a=
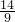
,不符合条件
当
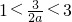
,即
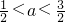
时,y的最小值在为3-
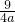
<8,不符合条件
当
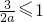
,即

时,y的最小值在x=1处取到,其值为a,令a=8解得a=8
综上知,当x∈[1,3]时有最小值8时,a的值为8
分析:(1)由对数的运算性质log
ab•log
ba=1及a>b>1,不难求出log
ab及log
ba的值,代入即可求出log
ab-log
ba的值.
(2)求二次函数在定区间上的最值,关键是要分析定区间也函数对称轴的关系,并结合函数的单调性进行分类讨论.
点评:二次函数y=ax
2+bx+c,在定区间[m,n]上,[1]当m≥-

时,对称轴在区间左侧,f (x)在[m,n]上递增,则f (x)的最大值为f (n),最小值为f (m);[2]当n≤-

时,对称轴在区间右侧,f (x) 在[m,n]上递减,,则f (x)的最大值为f (m),最小值为f(n);[3]当-

∈(m,n)时,则f(x)的最小值为f (-

);在[m,-

]上函数f (x)递减,则f (x)的最大值为f (m),在[-

,n]上函数f (x)递增,则f (x)的最大值为f (n),比较f (m)与f (n)的大小即得.

 ,求logab-logba的值.
,求logab-logba的值.

 =
=
 =
=

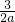 <0,
<0,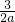 >0,
>0,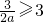 ,即
,即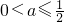 时,y的最小值在x=3处取到,最小值为9a-6,令9a-6=8,得a=
时,y的最小值在x=3处取到,最小值为9a-6,令9a-6=8,得a=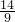 ,不符合条件
,不符合条件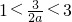 ,即
,即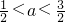 时,y的最小值在为3-
时,y的最小值在为3-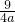 <8,不符合条件
<8,不符合条件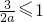 ,即
,即 时,y的最小值在x=1处取到,其值为a,令a=8解得a=8
时,y的最小值在x=1处取到,其值为a,令a=8解得a=8 时,对称轴在区间左侧,f (x)在[m,n]上递增,则f (x)的最大值为f (n),最小值为f (m);[2]当n≤-
时,对称轴在区间左侧,f (x)在[m,n]上递增,则f (x)的最大值为f (n),最小值为f (m);[2]当n≤- 时,对称轴在区间右侧,f (x) 在[m,n]上递减,,则f (x)的最大值为f (m),最小值为f(n);[3]当-
时,对称轴在区间右侧,f (x) 在[m,n]上递减,,则f (x)的最大值为f (m),最小值为f(n);[3]当- ∈(m,n)时,则f(x)的最小值为f (-
∈(m,n)时,则f(x)的最小值为f (- );在[m,-
);在[m,- ]上函数f (x)递减,则f (x)的最大值为f (m),在[-
]上函数f (x)递减,则f (x)的最大值为f (m),在[- ,n]上函数f (x)递增,则f (x)的最大值为f (n),比较f (m)与f (n)的大小即得.
,n]上函数f (x)递增,则f (x)的最大值为f (n),比较f (m)与f (n)的大小即得. 
