
| A. | [1,+∞) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,1] |
分析 求出定义域,再求出$\sqrt{{x}^{2}-4}$的值域,根据指数函数的性质求解值域.
解答 解:函数$y={3^{\sqrt{{x^2}-4}}}$,其定义域为{x|x≥2或x≤-2}.
令t=$\sqrt{{x}^{2}-4}$,
则t≥0,
∵函数$y={3^{\sqrt{{x^2}-4}}}$=3t是增函数,
∴当t=0时,函数y取得最小值为1,
所以函数$y={3^{\sqrt{{x^2}-4}}}$的值域为[1,+∞).
故选A.
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
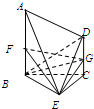 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
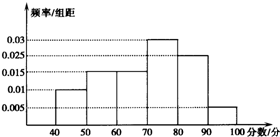 从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{81}+\frac{y^2}{16}=1$ | B. | x2+y2=1 | C. | $\frac{x^2}{27}+\frac{y^2}{8}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com