
分析 ①由函数奇偶性,周期性,对称性之间的关系,可知①正确;
②求导数,利用导数大于0,即可判断;
③求出f′($\frac{π}{4}$)=$\sqrt{2}$-1,可得f($\frac{π}{4}$)的值;
④函数f(x)=2x|log0.5x|-1的零点个数,即方程2x|log0.5x|-1=0根个数,即方程|log0.5x|=($\frac{1}{2}$)x根个数,即函数y=|log0.5x|与y=($\frac{1}{2}$)x图象交点的个数,画出函数图象,数形结合,可得答案.
解答 解:对于①,如函数对定义域内任意x都有f(x)=f(2-x),则是对称轴为1的函数,又为奇函数,所以是周期函数,且周期为4.所以正确.
对于②,f′(x)=(4-x)e-x>0,∴x<4,∴函数f(x)=(x-3)e-x的单调递增区间为(-∞,4),不正确;
③若函数f(x)=f'($\frac{π}{4}$)cosx+sinx,则f′(x)=-f'($\frac{π}{4}$)sinx+cosx,所以f′($\frac{π}{4}$)=-f'($\frac{π}{4}$)sin$\frac{π}{4}$+cos$\frac{π}{4}$,所以f′($\frac{π}{4}$)=$\sqrt{2}$-1,所以f($\frac{π}{4}$)的值为1,正确;
④函数f(x)=2x|log0.5x|-1的零点个数,
即方程2x|log0.5x|-1=0根个数,
即方程|log0.5x|=($\frac{1}{2}$)x根个数,
即函数y=|log0.5x|与y=($\frac{1}{2}$)x图象交点的个数,
在同一坐标系中画出函数y=|log0.5x|与y=($\frac{1}{2}$)x图象,如下图所示: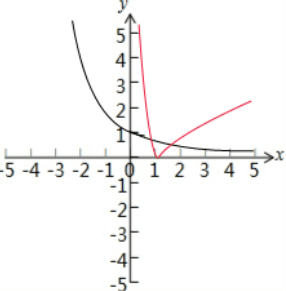
由图可得:函数y=|log0.5x|与y=($\frac{1}{2}$)x图象有2个交点,
故函数f(x)=2x|log0.5x|-1的零点有2个,正确.
故答案为:①③④.
点评 本题考查了命题真假的判断,考查学生分析解决问题的能力,综合性强,须认真审题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ②③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 表示该组上的个体在样本中出现的频率 | |
| B. | 表示取某数的频率 | |
| C. | 表示该组上的个体数与组距的比值 | |
| D. | 表示该组上的个体在样本中出现的频率与组距的比值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com