
| A. | ①④ | B. | ②③ | C. | ②③④ | D. | ②④ |
分析 利用复合命题的真假判断①的正误;命题的否定判断②的正误;直线与圆的位置关系判断③的正误;利用二项分布判断④的正误.
解答 解:对于①,若p∨q为真命题,则p,q至少有一个为真命题,①错误.
对于②,命题“?x0∈R,2x0≤0”的否定是?x∈R,2x>0,满足特称命题与全称命题的否定关系,正确.
对于③,直线l:y=kx+l恒过(0,1)点与圆O:x2+y2=1相交于A、B两点,则“k=±l”是△OAB的面积为$\frac{1}{2}$;
“k=l”是△OAB的面积为$\frac{1}{2}$的充分而不必要条件;正确;
对于④,随机变量ξ~N(0,1),已知Φ(-1.96)=0.025,则P(|ξ|<1.96)=P(-1.96<ξ<1.96)=1-2×0.025=0.95.④错误.
故选:B.
点评 标题考查命题的真假的判断,复合命题以及命题否定、充要条件等知识点,考查分析问题解决问题的能力.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
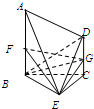 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{81}+\frac{y^2}{16}=1$ | B. | x2+y2=1 | C. | $\frac{x^2}{27}+\frac{y^2}{8}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n⊥α,则m∥α | B. | 若α⊥β,m∥α,则m⊥β | ||
| C. | 若m∥α,n∥β,m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $T=2π,{y_{max}}=2\sqrt{3}$ | B. | $T=π,{y_{max}}=2\sqrt{3}$ | C. | T=π,ymax=3 | D. | T=π,ymax=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 实验顺序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 零件数 x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 66 | 75 | 84 | 88 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com