考点:三角函数线
专题:数形结合,三角函数的求值
分析:在单位圆中画出三角函数线.
(1)由[0,2π)内,sin
=sin
=
,结合正弦线得sinα≥
的解集;
(2)由[0,2π)内,cos
=cos
=
,结合余弦线得cosα
≤的解集.
(3)由[0,2π)内,|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|sin
|=
,结合余弦线、正弦线得|cosα|>|sinα|的解集.
解答:
解:在单位圆内作三角函数线如图:
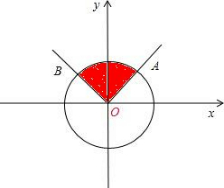
(1)∵在[0,2π)内,sin
=sin
=
,
OA,OB分别为
,
的终边,由正弦线可知,
满足sinα≥
的角的终边在劣弧AB内,
∴sinα≥
的解集为{α|
+2kπ≤α≤
+2kπ,k∈Z};
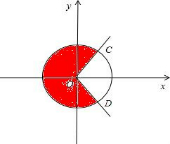
(2)∵在[0,2π)内,cos
=cos
=
,
OC,OD分别为
,
的终边,由余弦线可知,
满足cosα
≤的终边在劣弧CD内,
∴cosα
≤的解集为{α|
+2kπ≤α≤
+2kπ,k∈Z}.
(3)∵在[0,2π)内,|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|cos
|=|sin
|=|sin
|=
,
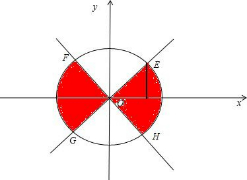
OE,OF,OG,OH分别为
,
,
,
的终边,由余弦线可知,
满足cosα
≤的终边在劣弧FG,EH内,
∴)|cosα|>|sinα|的解集为{α|kπ-
<α<kπ
+,k∈Z}.
点评:本题考查了三角函数线,考查了三角不等式的解法,考查了数形结合的解题思想方法,属于基本知识的考查.






 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案