
设函数f(x)=﹣ x3+2ax2﹣3a2x+b,0<a<1.
x3+2ax2﹣3a2x+b,0<a<1.
(1)求函数f(x)的单调区间、极值;
(2)若x∈[0,3a],试求函数f(x)的最值.
(1)函数f(x)的单调减区间为(﹣∞,a),(3a,+∞),单调增区间为(a,3a).当x=a时,f(x)的极小值为﹣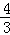 a3+b;当x=3a时,f(x)的极大值为b.
a3+b;当x=3a时,f(x)的极大值为b.
(2)当x=a时,f(x)的最小值为﹣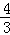 a3+b;当x=0或x=3a时,f(x)的最大值为b.
a3+b;当x=0或x=3a时,f(x)的最大值为b.
【解析】
试题分析:(1)要求函数f(x)的单调区间,即求函数f(x)的f′(x),令f′(x)=0,解出x,再根据导数与单调性的关系求解即可得到函数f(x)的单调区间、极值;
(2)由(1)知函数当x∈(0,a)时,函数f(x)为减函数;当x∈(a,3a)时,函数f(x)为增函数.进而得到函数f(x)在[0,3a]上的最值.
【解析】
(1)f′(x)=﹣x2+4ax﹣3a2.令f′(x)=0,解得x=a或x=3a,列表:
x | (﹣∞,a) | a | (a,3a) | 3a | (3a,+∞) |
f′(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 递减 | ﹣ | 递增 | b | 递减 |
由表可知:当x∈(﹣∞,a)时,函数f(x)为减函数;当x∈(3a,+∞)时,函数f(x)也为减函数;当x∈(a,3a)时,函数f(x)为增函数.
∴函数f(x)的单调减区间为(﹣∞,a),(3a,+∞),单调增区间为(a,3a).当x=a时,f(x)的极小值为﹣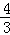 a3+b;当x=3a时,f(x)的极大值为b.
a3+b;当x=3a时,f(x)的极大值为b.
(2)x∈[0,3a],列表如下:
x | 0 | (0,a) | a | (a,3a) | 3a |
f′(x) |
| ﹣ | 0 | + | 0 |
f(x) | b | 递减 | ﹣ | 递增 | b |
由表知:当x∈(0,a)时,函数f(x)为减函数;当x∈(a,3a)时,函数f(x)为增函数.
∴当x=a时,f(x)的最小值为﹣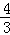 a3+b;当x=0或x=3a时,f(x)的最大值为b.
a3+b;当x=0或x=3a时,f(x)的最大值为b.


科目:高中数学 来源:[同步]2014年苏教版必修三 2.3 总体特征数的估计练习卷(解析版) 题型:解答题
某医院为了了解病人每分钟呼吸次数,对20名病人进行测量,记录结果如下:
12,20,16,18,20,28,23,16,15,18,20,24,18,21,18,19,18,31,18,13,
求这组数据的平均数,中位数,众数.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷(解析版) 题型:选择题
集合M={x|x∈Z且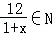 },则M的非空真子集的个数是( )
},则M的非空真子集的个数是( )
A.30个 B.32个 C.62个 D.64个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
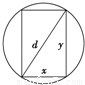
横梁的强度和它的矩形横断面的宽成正比,并和矩形横断面的高的平方成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的宽是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
某工厂要围建一个面积为512平方米的矩形堆料场,一边可以利用原有的墙壁,其它三边需要砌新的墙壁,当砌壁所用的材料最省时,堆料场的长和宽分别为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:填空题
(3分)已知函数f(x)= x4﹣2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是 .
x4﹣2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:填空题
(2008•上海)若直线ax﹣y+1=0经过抛物线y2=4x的焦点,则实数a= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com