
| A. | {z|-1≤z≤1} | B. | {z|-1≥z或z≥1} | C. | {z|-1<z<1} | D. | {z|-1>z或z>1} |
分析 如图所示,画出可行域$z=\frac{b+2}{2a-2}$即为2z=$\frac{b+2}{a-1}$表示可行域内的点P(a,b)与Q(1,-2)所在直线的斜率的2倍.分别求出直线OQ,BQ的斜率即可.
解答 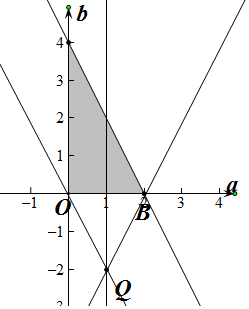 解:由$\left\{\begin{array}{l}{2a+b<4}\\{a>0}\\{b>0}\end{array}\right.$,$z=\frac{b+2}{2a-2}$即为2z=$\frac{b+2}{a-1}$表示可行域内的点P(a,b)与Q(1,-2)所在直线的斜率的2倍,
解:由$\left\{\begin{array}{l}{2a+b<4}\\{a>0}\\{b>0}\end{array}\right.$,$z=\frac{b+2}{2a-2}$即为2z=$\frac{b+2}{a-1}$表示可行域内的点P(a,b)与Q(1,-2)所在直线的斜率的2倍,
∵kOQ=-2,kQB=$\frac{0+2}{2-1}$=2,
∴z<-1或z>1,
故选:D.
点评 本题考查了线性规划的可行域、斜率计算公式,考查了推理能力与计算能力,考查了数形结合的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | ||||
| 爱好 | 40 | 20 | |||
| 不爱好 | 20 | 30 | |||
| P(K2≥k) | 0.050 | 0.010 | 0.001 | ||
| k | 3.841 | 6.635 | 10.828 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -2 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x^2}\;\;,\;\;g(x)=x$ | B. | $f(x)=\sqrt{x^2}\;,\;\;g(t)=\left\{\begin{array}{l}t,t≥0\\-t,t<0\end{array}\right.$ | ||
| C. | $f(x)=\root{3}{x^3}\;\;,\;\;g(x)=|x|$ | D. | $f(t)=t\;,\;\;g(x)=\frac{x^2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11π}{12}$ | B. | $\frac{5π}{6}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
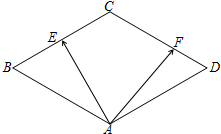
| A. | $\frac{1}{2}$ | B. | 2 | C. | 1 | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com