
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由相关系数与相关关系的关系判断①;由回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$一定通过样本点的中心判断②;根据统抽样方法的公平性即抽样过程中每个个体被抽到的概率是相等的判断③;根据方差的意义判断④.
解答 解:①统计中用相关系数r来衡量两个变量之间的线性关系的强弱.线性相关系数|r|越大,两个变量的线性相关性越强;反之,线性相关性越弱,①错误.
②回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$一定通过样本点的中心$(\overline x,\overline y)$,②正确.
③为了了解某地区参加数学竞赛的1003名学生的成绩情况,准备从中抽取一个容量为50的样本,现采用系统抽样的方法,需要从总体中剔除3个个体,在整体抽样过程中,每个个体被剔除的概率和每个个体被抽到的概率分别是$\frac{3}{1003}$和$\frac{50}{1003}$,③错误.
④将一组数据中每个数都加上或者减去同一个常数后,方差恒不变,④正确.
∴正确的命题有2个.
故选:C.
点评 本题考查命题的真假判断与应用,关键是对统计知识的熟练掌握,是基础题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {3} | C. | {2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4≤a≤9 | B. | a≤-4或a≥9 | C. | -9≤a≤4 | D. | a≤-9或a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
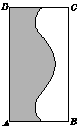 如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )
如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )| A. | 1.4 | B. | 1.6 | C. | 2.6 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
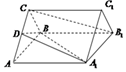 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 3 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com