【答案】
分析:(I)求出f(x)的导函数,把切点的横坐标x=1代入导函数求出切线的斜率,把x=1代入f(x)求出切点的纵坐标,根据切点坐标和斜率写出切线的方程,然后找出圆心坐标和圆的半径r,利用点到直线的距离公式表示出圆心到切线的距离d,让d等于r列出关于a的方程,求出方程的解即可得到a的值;
(II)当x=0时,显然f(x)=e
x>0恒成立;当x大于0时,令f(x)大于0,解出a大于一个函数,设这个函数为Q(x),求出Q(x)的导函数,分x大于0小于1和x大于1两种情况讨论导函数的正负,进而得到函数的增减性,根据函数的增减性得到Q(x)的最大值,即可得到a的取值范围;
(III)把f(x)和g(x)的解析式代入y中确定出y的解析式,设M(x)为y的解析式,求出M(x)的导函数,h(x)=
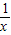
+lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x
∈[1,e],使曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直.
解答:解:(I)f′(x)=e
x+a,因此过点(1,f(1))的直线斜率为e+a,
又f(1)=e+a,∴过点(1,f(1))的直线方程为:y-(e+a)=(e+a)(x-1),
即(a+e)x-y=0,又已知圆的圆心为(1,0),半径为
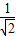
,
依题意,则有
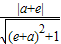
=
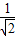
,解得a=-e+1,a=-e-1;
(II)∵在x≥0时,f(x)=e
x+ax>0恒成立,
若x=0,a为任意实数,f(x)=e
x>0恒成立,
若x>0,f(x)=e
x+ax>0恒成立,即a>-
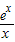
在x>0上恒成立,
设Q(x)=-
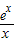
,Q′(x)=-
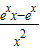
=
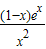
,
当x∈(0,1)时,Q′(x)>0,Q(x)在(0,1)上单调递增;
当x∈(1,+∞)时,Q′(x)<0,Q(x)在(1,+∞)上单调递减,
∴当x=1时,Q(x)取得最大值,Q(x)
max=Q(1)=-e,
∴要使x≥0时,f(x)=e
x+ax>0恒成立,a的取值范围是(-e,+∞);
(III)依题意,曲线C的方程为:y=e
xlnx-e
x+x,
令M(x)=e
xlnx-e
x+x,则M′(x)=
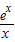
+e
xlnx-e
x+1=(

+lnx-1)e
x+1,
设h(x)=
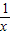
+lnx-1,则h′(x)=-
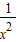
+
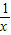
=
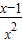
,
当x∈[1,e]时,h′(x)≥0,故h(x)为增函数,
因此,h(x)在区间[1,e]上的最小值为h(1)=ln1=0,
则M′(x)≥1,即曲线C:y=g(x)-f(x)在点x=x
处的切线的斜率k≥1,
故不存在实数x
∈[1,e],使曲线C:y=g(x)-f(x)在点x=x
处的切线与y轴垂直.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握直线与圆的位置关系的判别方法,掌握导数在最大值、最小值中的运用,是一道中档题.

 相切,求a的值;
相切,求a的值;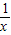 +lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x∈[1,e],使曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直.
+lnx-1,求出h(x)的导函数,由x的范围得到导函数为正数,进而得到h(x)在[1,e]上为增函数,得到h(1)为最小值,即可得到M(x)的最小值,而曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直,即切线的斜率为0,即导函数的值为0,与导函数的最小值为1矛盾,所以不存在实数x∈[1,e],使曲线C:y=g(x)-f(x)在点x=x处的切线与y轴垂直.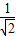 ,
,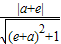 =
=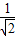 ,解得a=-e+1,a=-e-1;
,解得a=-e+1,a=-e-1;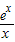 在x>0上恒成立,
在x>0上恒成立,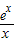 ,Q′(x)=-
,Q′(x)=-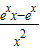 =
=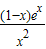 ,
,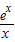 +exlnx-ex+1=(
+exlnx-ex+1=( +lnx-1)ex+1,
+lnx-1)ex+1,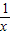 +lnx-1,则h′(x)=-
+lnx-1,则h′(x)=-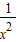 +
+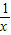 =
=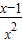 ,
,

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案