
【题目】已知点M是圆C:(x+1)2+y2=8上的动点,定点D(1,0),点P在直线DM上,点N在直线CM上,且满足![]() 2
2![]() ,
,![]()
![]() 0,动点N的轨迹为曲线E.
0,动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)由已知得NP为DM的垂直平分线,|ND|=|NM|,![]() ,由此能求了轨迹E的方程.
,由此能求了轨迹E的方程.
(2)法一:设直线AB的方程为y=kx+m,由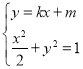 ,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
(2)法二:设直线AB的方程为y=kx+m,由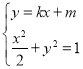 ,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
(1)解:因为![]() ,
,![]() ,
,
所以NP为DM的垂直平分线,
所以|ND|=|NM|,又因为![]() ,
,
所以![]()
所以动点N的轨迹是以点C(﹣1,0),D(1,0)为焦点的长轴为![]() 的椭圆.
的椭圆.
所以轨迹E的方程为![]() .
.
(2)解法一:因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,
则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+m,
由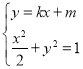 ,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
设A(x1,y1),B(x2,y2),又△=16k2m2﹣4(1+2k2)(2m2﹣2)>0,
所以![]() ,
,![]()
因为|AB|=2,所以![]() ,即
,即![]()
所以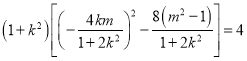 ,即
,即![]() ,
,
因为1+k2≥1,所以![]() .
.
又点O到直线AB的距离![]() ,
,
因为![]() h,
h,
所以S2=h2=2m2(1﹣m2)![]()
所以![]() ,即S的最大值为
,即S的最大值为![]() .
.
(2)解法二:因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,
则弦AB不能与x垂直,故可设直线AB的方程为y=kx+m,
由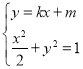 ,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
设A(x1,y1),B(x2,y2),又△=16k2m2﹣4(1+2k2)(2m2﹣2)>0,
所以![]() ,
,![]() .
.
因为|AB|=2,所以![]() .
.
因为![]() ,
,
所以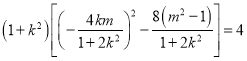 ,
,
所以 ,
,
又点O到直线AB的距离![]() ,所以
,所以![]() h.
h.
所以S2=h2 .
.
设![]() ,则
,则![]() ,
,
所以![]() ,即S的最大值为
,即S的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中曲线C的参数方程为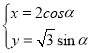 (
(![]() 为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为
为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l过A,B两点,且这两点的极坐标分别为![]() .
.
(I)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(II)若M为曲线C上一动点,求点M到直线l的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某校某班44名同学的某次考试的物理成绩y和数学成绩x的散点图:
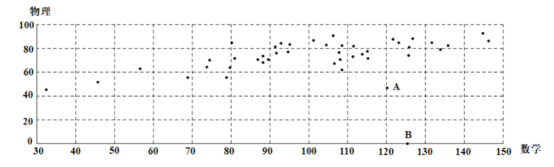
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计量的值:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() .y与x的相关系数
.y与x的相关系数![]() .
.
(1)若不剔除A、B两名考生的数据,用44数据作回归分析,设此时y与x的相关系数为![]() ,试判断
,试判断![]() 与r的大小关系,并说明理由;
与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到![]() ),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
),并估计如果B考生参加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位).
附:回归方程![]() 中,
中, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
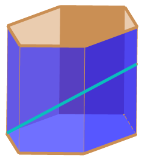
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com