
(本小题满分12分)已知 
(1)求 的最小值;
的最小值;
(2)求 的值域。
的值域。
(1) 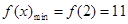 ; (2)
; (2) 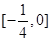 。
。
解析试题分析:(I)先根据 ,得到
,得到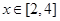 ,再结合二次函数的单调性可知f(x)在x=2处取得最小值。
,再结合二次函数的单调性可知f(x)在x=2处取得最小值。
(II)可以采用换元法令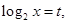 则
则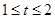 ,所以原函数可转化为
,所以原函数可转化为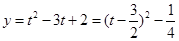 二次函数最值问题研究。
二次函数最值问题研究。
(1) ∵ 
∴ 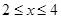 ……………………………………………………………2分
……………………………………………………………2分
又 在[2,4]上单调递增………………………………3分
在[2,4]上单调递增………………………………3分
所以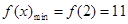 …………………………………………………5分
…………………………………………………5分
(2) ∵  =(
=(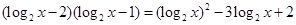
………………………………………………8分
设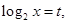 则
则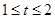
则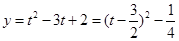 ……………………………………………10分
……………………………………………10分
所以可知当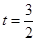 时,即
时,即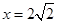 时,
时,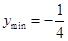
当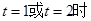 ,即
,即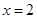 或4时,
或4时,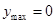
∴  的值域为
的值域为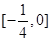 ……………………………12分
……………………………12分
考点:对数不等式,一元二次函数的最值,及换元法。
点评:掌握一元二次函数的性质是解本题的关键,其中知道对称轴两侧单调性相同,对称轴一侧才具有单调性。


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
(本小题12分)已知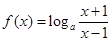 (
(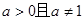 ).
).
(1)判断函数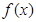 的奇偶性,并证明;
的奇偶性,并证明;
(2)若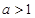 ,用单调性定义证明函数
,用单调性定义证明函数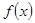 在区间
在区间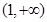 上单调递减;
上单调递减;
(3)是否存在实数 ,使得
,使得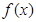 的定义域为
的定义域为 时,值域为
时,值域为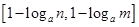 ,若存在,求出实数
,若存在,求出实数 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,已知前30天价格为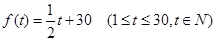 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
(I)写出该种商品的日销售额S与时间t的函数关系式;
(II)求日销售额S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com