(本小题满分12分)经市场调查，某种商品在过去50天的销售量和价格均为销售时间t（天）的函数，已知前30天价格为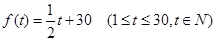
，后20天价格为f（t）="45" （31£ t £50, tÎN）,且销售量近似地满足g（t）=" -2t+200" （1£t£50, tÎN）．
（I）写出该种商品的日销售额S与时间t的函数关系式；
（II）求日销售额S的最大值．
（1）s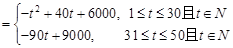
；②日销售额S的最大值为6400．
解析试题分析：（1）因为价格与销售的天数不是同一函数，因此根据销售额等于销售量乘以售价得S与t的函数关系式，此关系式为分段函数；
（2）求出分段函数的最值即可．
（1）根据题意得：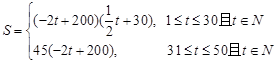
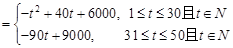……………6分
（2）①当1£ t£30且tÎN时，S= -（t-20）2+6400∴当t=20时 Smax=6400………………………8分
②当31£ t£50且tÎN时，S= -90t+9000为减函数∴当t=31时 Smax=6210………………………10分
又∵6210<6400 ∴当t=20时 Smax=6400 答：日销售额S的最大值为6400．……12分
考点：根据实际问题正确建立数学模型，函数的最值问题及其代表的实际意义.
点评：加强对应用题的训练，增加数学建模能力，是解决应用题的必由之路.
科目：高中数学 来源： 题型：解答题
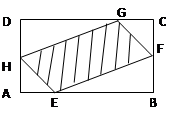
（本题满分12分） 如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝
（>2），BC＝2，且AE＝AH＝CF＝CG，设AE＝
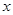，绿地面积为
.
（1）写出关于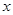的函数关系式，并指出这个函数的定义域;
（2）当AE为何值时，绿地面积最大？ （10分）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
已知函数
定义域为
，若对于任意的
，都有
，且
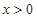时，有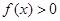
.
（1）求证: 为奇函数;
（2）求证: 在上为单调递增函数;
（3）设
,若<
,对所有
恒成立,求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(12分)已知函数f(x)＝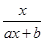
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，问方程
在区间[－1，0]内是否有
在(0,1)内恰有一解，求实数
的取值范围． 
在区间
上存在零点；Q：函数
在
内没有极值点．若“P或Q”为真命题，“P且Q”为假命题，求实数
的取值范围.
,
，使得
，求实数
的取值范围；
，且
在区间
上单调递增，求实数
的最小值； 
的值域。
，
的定义域为R，求实数
的取值范围.