
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于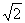 。
。
(1)求动点M的轨迹方程,并说明它表示什么曲线;
(2)若直线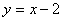 与曲线相交于AB两点,求弦AB的长。
与曲线相交于AB两点,求弦AB的长。
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
设f(x)是定义在R上的增函数,且对于任意的x都有f(-x)+f(x)=0恒成立.如果实数m、n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是___________.
|
查看答案和解析>>
科目:高中数学 来源: 题型:
设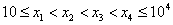 ,
,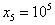 . 随机变量
. 随机变量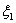 取值
取值 、
、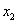 、
、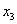 、
、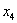 、
、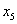 的概率均为0.2,随机变量
的概率均为0.2,随机变量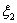 取值
取值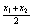 、
、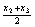 、
、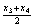 、
、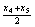 、
、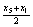 的概率也为0.2.
的概率也为0.2.
若记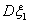 、
、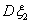 分别为
分别为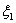 、
、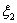 的方差,则 ( )
的方差,则 ( )
A.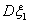 >
>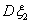 . B.
. B.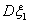 =
=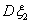 . C.
. C.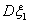 <
<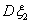 .
.
D.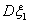 与
与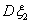 的大小关系与
的大小关系与 、
、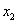 、
、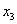 、
、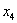 的取值有关.
的取值有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数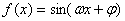 (
(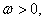
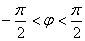 ),给出以下四个论断:①它的图像关于直线
),给出以下四个论断:①它的图像关于直线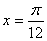 对称;②它的图像关于点(
对称;②它的图像关于点(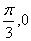 )对称;③它的最小正周期是
)对称;③它的最小正周期是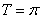 ;④它在区间
;④它在区间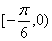 上是增函数.以其中的两个论断作为条件,余下的两个论断作为结论,写出你认为正确的两个命题,并对其中的一个命题加以证明
上是增函数.以其中的两个论断作为条件,余下的两个论断作为结论,写出你认为正确的两个命题,并对其中的一个命题加以证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com