
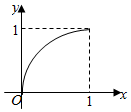
 已知幂函数y=f(x),f′(x)为f(x)的导函数,f(x)在区间[0,1]上图象如图所示.对满足:0<x1<x2<1的任意x1、x2,给出下列结论:
已知幂函数y=f(x),f′(x)为f(x)的导函数,f(x)在区间[0,1]上图象如图所示.对满足:0<x1<x2<1的任意x1、x2,给出下列结论:| A. | ①②③ | B. | ①③ | C. | ③④ | D. | ②③ |
分析 由函数的图象,我们可根据$\frac{f{(x}_{2})-f{(x}_{1})}{{x}_{2}{-x}_{1}}$(图象上任意两点之间的斜率)与1的大小判断①的对错;根据得$\frac{f{(x}_{1})}{{x}_{1}}$与$\frac{f{(x}_{2})}{{x}_{2}}$(图象上任意两点与原点连线的斜率)的大小判断②的正误;再根据函数图象是凸增的,我们可判断③的真假;得到f′(x)在(0,1)递减,由x1<x2得:f′(x1)>f′(x2),(x1-x2)<0,从而判断正误.
解答 解:由f(x2)-f(x1)>x2-x1,可得 $\frac{f{(x}_{2})-f{(x}_{1})}{{x}_{2}{-x}_{1}}$>1,
即两点(x1,f(x1))与(x2,f(x2))连线的斜率大于1,
显然①不正确;
由x2f(x1)>x1f(x2),得 $\frac{f{(x}_{1})}{{x}_{1}}$>$\frac{f{(x}_{2})}{{x}_{2}}$,
即表示两点(x1,f(x1))、(x2,f(x2))与原点连线的斜率的大小,
可以看出结论②正确;
结合函数图象,容易判断③的结论是正确的,
结合图象函数递增的速度减小,故f′(x)在(0,1)递减,
由x1<x2得:f′(x1)>f′(x2),即f′(x1)-f′(x2)>0,(x1-x2)<0,
故④[f′(x1)-f′(x2)](x1-x2)<0,④错误;
故选:D.
点评 本题考查的知识点是函数的图象和直线的斜率,解答的关键是结合函数图象分析结论中式子的几何意义,然后进行判断.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
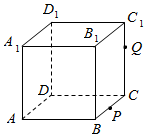 如图所示,正方体ABCD-A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点,过点A、P、Q的平面截正方体所得的截面即为S.
如图所示,正方体ABCD-A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点,过点A、P、Q的平面截正方体所得的截面即为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
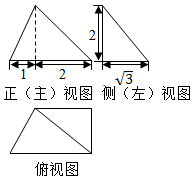
| A. | $\sqrt{5}∈A$ | B. | $\sqrt{11}∈A$ | C. | $\sqrt{7}∈A$ | D. | 4∈A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com