某程序框图如图所示.其中t∈Z.该程序运行后输出的k=4.则t的最大值为( )A．10B．11C．12D．13 题目和参考答案——青夏教育精英家教网—

6．某程序框图如图所示，其中t∈Z，该程序运行后输出的k=4，则t的最大值为（　　）

A．

B．

C．

D．

分析执行程序框图，写出每次循环得到的S，k的值，输出k的值为4，可得3≤t＜11，结合t∈Z，即可求得t的最大值为10．

解答解：模拟程序的运行，可得
k=10，S=0
满足条件S≤t，执行循环体，S=1，k=8
满足条件S≤t，执行循环体，S=3，k=6
满足条件S≤t，执行循环体，S=11，k=4
由题意，此时，应该不满足条件S≤t，退出循环，输出k的值为4．
所以：3≤t＜11，由于t∈Z，则t的最大值为10．
故选：A．

点评本题主要考察了程序框图和算法的应用，解题时要认真审题，仔细解答，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

16．

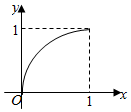已知幂函数y=f（x），f′（x）为f（x）的导函数，f（x）在区间[0，1]上图象如图所示．对满足：0＜x₁＜x₂＜1的任意x₁、x₂，给出下列结论：
①f（x₁）-f（x₂）＞x₁-x₂
②x₂f（x₁）＞x₁f（x₂）
③$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$＜f（$\frac{{x}_{1}+{x}_{2}}{2}$）
④[f′（x₁）-f′（x₂）]（x₁-x₂）＞0
其中一定正确结论的序号是（　　）

A．

①②③

B．

①③

C．

③④

D．

②③

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．若f（x）=x³-$\frac{9}{2}$x²+6x-5满足条件f′（x）≥m恒成立，则m的最大值是-$\frac{3}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．已知椭圆C：2x²+y²=16．
（1）求椭圆C的离心率；
（2）设O为原点，点A在椭圆C上，点B在直线x=4上，且$\overrightarrow{OA}•\overrightarrow{OB}$=0，求直线AB截圆x²+y²=17所得弦长为l．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．已知抛物线C：y²=2px（p＞0）上的一点M（3，t）到焦点的距离为5．
（Ⅰ）求抛物线C的方程；
（Ⅱ）过点T（-2，0）的直线l与抛物线C交于A，B两点，若在x轴上存在一点E，使得△EAB是以点E为直角顶点的直角三角形，求直线l的斜率的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．在△ABC中，内角A，B，C的对边分别为a，b，c，且2c-2acosB=b．
（1）求角A的大小；
（2）若△ABC的面积为$\frac{\sqrt{3}}{4}$，且c²+abcosC+a²=4，求a．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．将函数y=sin（-2x）+cos（2x）的图象（　　）得到函数y=$\sqrt{2}$sin（-2x）的图象．

	A．	向左平移$\frac{π}{8}$个单位		B．	向右平移$\frac{π}{8}$个单位
	C．	向左平移$\frac{π}{4}$个单位		D．	向右平移$\frac{π}{4}$个单位

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．

如表是一个由n²个正数组成的数表，用a_ij表示第i行第j个数（i，j∈N），已知数表中第一列各数从上到下依次构成等差数列，每一行各数从左到右依次构成等比数列，且公比都相等．已知a₁₁=1，a₃₁+a₆₁=9，a₃₅=48．
（1）求a_n1和a_4n；
（2）设c_n=$\frac{{2{a_{n1}}}}{{{a_{4n}}}}$，求数列{c_n}的前n项和S_n．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．已知A、B为双曲线E的左右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为$\sqrt{2}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学