
 如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.
如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.分析 (1)设第1列依次组成的等差公差为d,设第1行依次组成的等比数列的公比为q,根据题意可以求出d和q,再根据通项公式的定义即可求出;
(2)根据错位相减法即可求出前n项和.
解答 解:(1)设第1列依次组成的等差公差为d,设第1行依次组成的等比数列的公比为q,根据题意a31+a61=(1+2d)+(1+5d)=9,
∴d=1,
∴an1=a11+(n-1)d=1+(n-1)×1=n,
∵a31=a11+2d=3,
∴a35=a31,q4=3q4=48,
∵q>0,
∴q=2,
∵a41=4,
∴a4n=a41qn-1=4×2n-1=2n+1,
(2)Cn=$\frac{{2{a_{n1}}}}{{{a_{4n}}}}$=$\frac{2n}{{2}^{n+1}}$=$\frac{n}{{2}^{n}}$,
∴Sn=1×$\frac{1}{2}$+2×$\frac{1}{{2}^{2}}$+…+(n-1)×$\frac{1}{{2}^{n-1}}$+n×$\frac{1}{{2}^{n}}$,
∴$\frac{1}{2}$Sn=1×$\frac{1}{{2}^{2}}$+…+(n-2)×$\frac{1}{{2}^{n-1}}$+(n-1)×$\frac{1}{{2}^{n}}$+n×$\frac{1}{{2}^{n+1}}$
作差$\frac{1}{2}$Sn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-n×$\frac{1}{{2}^{n+1}}$=1-$\frac{n+2}{{2}^{n+1}}$
∴Sn=2-$\frac{n+2}{{2}^{n}}$
点评 本题考查了数列通项公式的求法和错位相减法求前n项和,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
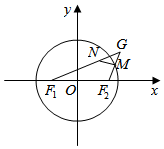 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 天数x | 3 | 4 | 5 | 6 | 7 |
| 繁殖数(千个) | 2.5 | 3 | t | 4.5 | 6 |
| A. | 3.5 | B. | 3.75 | C. | 4 | D. | 4.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com