
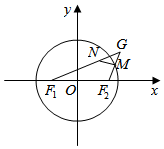
 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.分析 (1)连接NF2,则|NF2|=|NG|,利用椭圆的定义,即可求椭圆E的方程;
(2)PA⊥PB,设P(x0,y0),将直线AD的方程y=$\frac{{y}_{0}}{4{x}_{0}}$(x+x0)-y0代入椭圆的方程,并整理,求出B的坐标,证明kPA•kPB=-1,即可得到结论.
解答  解:(1)连接NF2,则|NF2|=|NG|,
解:(1)连接NF2,则|NF2|=|NG|,
∴|NF1|+|NF2|=|F1G|.
连接OM,则|F1G|=2|OM|=4,
∴|NF1|+|NF2|=4>|F1F2|,
∴点N的轨迹是以F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为焦点的椭圆,且2a=4,2c=2$\sqrt{3}$,
∴a=2,c=$\sqrt{3}$,
∴b=1,
∴点N的轨迹方程E:$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(2)PA⊥PB.
证明:设P(x0,y0),则A(-x0,-y0),D(x0,-$\frac{1}{2}$y0)且x02+4y02=4
将直线AD的方程y=$\frac{{y}_{0}}{4{x}_{0}}$(x+x0)-y0代入椭圆的方程,
并整理得(4x02+y02)x-6x0y02+9x02y02-16x02=0
由题意,可知此方程必有一根-x0,
xB=$\frac{6{x}_{0}{{y}_{0}}^{2}}{4{{x}_{0}}^{2}+{{y}_{0}}^{2}}$+x0,yB=$\frac{{{y}_{0}}^{3}-2{{x}_{0}}^{2}{y}_{0}}{4{{x}_{0}}^{2}+{{y}_{0}}^{2}}$,
所以kPB=$\frac{\frac{{{y}_{0}}^{3}-2{{x}_{0}}^{2}{y}_{0}}{4{{x}_{0}}^{2}+{{y}_{0}}^{2}}-{y}_{0}}{\frac{6{x}_{0}{{y}_{0}}^{2}}{4{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$=$\frac{-6{{x}_{0}}^{2}{y}_{0}}{6{x}_{0}{{y}_{0}}^{2}}$=-$\frac{{x}_{0}}{{y}_{0}}$
故有kPA•kPB=-1,即PA⊥PB.
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m?β,则α⊥β | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m⊥β,m⊥α,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.
如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,当多项式为x4+4x3+6x2+4x+1时,求解它的值所反映的程序框图如图所示,当x=1时输出的结果为( )
我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,当多项式为x4+4x3+6x2+4x+1时,求解它的值所反映的程序框图如图所示,当x=1时输出的结果为( )| A. | 15 | B. | 5 | C. | 16 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com