
分析 (1)化椭圆方程为标准式,求出a,b的值,利用隐含条件求得c,则椭圆离心率可求;
(2)依题意设(x0,y0),B(4,t),由$\overrightarrow{OA}•\overrightarrow{OB}$=0,把B的坐标用A的坐标表示,写出过A、B的点斜式方程,由点到直线的距离公式求出坐标原点O到AB的距离,再由垂径定理求得直线AB截圆x2+y2=17所得弦长.
解答 解:(1)由椭圆C:2x2+y2=16,得$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{16}=1$,
∴$a=4,b=2\sqrt{2}$,则$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{16-8}=2\sqrt{2}$.
故椭圆C的离心率为e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
(2)设A(x0,y0),B(4,t),
∴$\frac{{{x}_{0}}^{2}}{8}+\frac{{{y}_{0}}^{2}}{16}=1$,①
由$\overrightarrow{OA}•\overrightarrow{OB}$=0,得$t=\frac{4{x}_{0}}{-{y}_{0}}$,②
根据点斜式得到直线AB的方程为:y-t=$\frac{{y}_{0}-t}{{x}_{0}-4}(x-4)$,化简得
(y0-t)x-(x0-4)y-4y0+tx0=0.
原点O到AB的距离d=$\frac{|-4{y}_{0}+t{x}_{0}|}{\sqrt{({y}_{0}-t)^{2}+({x}_{0}-4)^{2}}}$.
将①②代入可得:d=$\frac{|-4{y}_{0}+t{x}_{0}|}{\sqrt{({y}_{0}-t)^{2}+({x}_{0}-4)^{2}}}$=$\frac{|4{y}_{0}-\frac{4{x}_{0}}{-{y}_{0}}|}{\sqrt{{{y}_{0}}^{2}-2•\frac{4{x}_{0}}{-{y}_{0}}•{y}_{0}+{{x}_{0}}^{2}-8{x}_{0}+16}}$
=$\frac{|4{{y}_{0}}^{2}+4{{x}_{0}}^{2}|}{\sqrt{{{y}_{0}}^{4}+16{{x}_{0}}^{2}+{{x}_{0}}^{2}{{y}_{0}}^{2}+16{{y}_{0}}^{2}}}$=$\frac{|2{{y}_{0}}^{2}+32|}{\sqrt{\frac{1}{2}({{y}_{0}}^{2}+16)^{2}}}=2\sqrt{2}•\frac{{{y}_{0}}^{2}+16}{{{y}_{0}}^{2}+16}=2\sqrt{2}$.
在圆x2+y2=17中,利用勾股定理可得$\frac{l}{2}=\sqrt{17-(2\sqrt{2})^{2}}=3$.
∴直线AB截圆x2+y2=17所得弦长为6.
点评 本题考查椭圆的简单性质,考查了直线与圆锥曲线位置关系的应用,考查计算能力,是中档题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
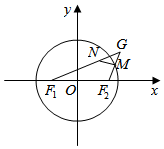 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com