
分析 (Ⅰ)将Q的坐标代入椭圆方程,以及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)求出直线l与x,y轴的交点,代入椭圆方程,运用韦达定理,以及向量共线的坐标表示,可得k的值;
(Ⅲ)由切线的性质,结合四点共圆判断可得P,P1,O,P2四点共圆,可得其圆心O'($\frac{{x}_{P}}{2}$,$\frac{{y}_{P}}{2}$),求得圆方程,由两圆方程相减可得相交弦方程,由题意可得P1P2的方程为$\frac{x}{m}$+$\frac{y}{n}$=1,求得P的坐标,代入椭圆方程即可得证.
解答 解:(Ⅰ)椭圆过点Q($\sqrt{2}$,1),
可得$\frac{2}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,由题意可得c=$\sqrt{2}$,即a2-b2=2,
解得a=2,b=$\sqrt{2}$,
即有椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(Ⅱ)直线l:y=k(x-1)与x轴交点C(1,0),y轴交点D(0,-k),
联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=4}\\{y=k(x-1)}\end{array}\right.$,消y得,(1+2k2)x2-4k2x+2k2-4=0,①
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,
$\overrightarrow{CN}$=(x2-1,y2),$\overrightarrow{MD}$=(-x1,-k-y1),
由$\overrightarrow{CN}=\overrightarrow{MD}$,得:x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$=1,
解得k=±$\frac{\sqrt{2}}{2}$;
(Ⅲ)证明:因为P1,P2为切点,所以OP1⊥PP1,OP2⊥PP2,
所以P,P1,O,P2四点共圆,
其圆心O'($\frac{{x}_{P}}{2}$,$\frac{{y}_{P}}{2}$),方程为(x-$\frac{{x}_{P}}{2}$)2+(y-$\frac{{y}_{P}}{2}$)2=$\frac{{{x}_{P}}^{2}+{{y}_{P}}^{2}}{4}$,
整理得x2+y2-xxP-yyP=0,
P1,P2是圆O与圆O'的交点,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=2}\\{{x}^{2}+{y}^{2}-x{x}_{P}-y{y}_{P}=0}\end{array}\right.$得xxP+yyP=2,
直线P1P2在x轴,y轴上的截距分别为m,n,
可得直线P1P2的方程为$\frac{x}{m}$+$\frac{y}{n}$=1,
得xP=$\frac{2}{m}$,yP=$\frac{2}{n}$,
因为P(xP,yP)在椭圆x2+2y2=4上,
则($\frac{2}{m}$)2+2($\frac{2}{n}$)2=4,
整理得$\frac{1}{m^2}+\frac{2}{n^2}$=1.
点评 本题考查椭圆方程的求法,注意运用点满足椭圆方程,考查直线方程和椭圆方程联立,运用韦达定理和向量相等的条件,同时考查圆方程的求法,以及两圆相交弦的问题,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
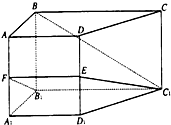 如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB═$\sqrt{2}$,AD=2,BC=4,AA1=2,E,F分别是DD1,AA1的中点.
如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB═$\sqrt{2}$,AD=2,BC=4,AA1=2,E,F分别是DD1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,-3] | B. | (-∞,-$\frac{9}{8}$] | C. | (-∞,-2] | D. | [-4,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 60°或120° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m?β,则α⊥β | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m⊥β,m⊥α,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com