
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
分析 展开($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=0,代入数量积公式即可求得向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角.
解答 解:设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,
由|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=0,
得$\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=|\overrightarrow{a}|•|\overrightarrow{b}|cosθ+|\overrightarrow{b}{|}^{2}=0$,
即2×1×cosθ=-1,
∴cos$θ=-\frac{1}{2}$.
∵θ∈[0°,180°],
∴θ=120°.
故选:D.
点评 本题考查平面向量的数量积运算,考查了由数量积求斜率的夹角,是中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
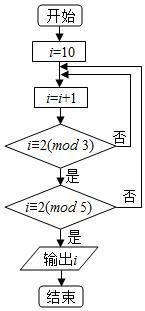 把“正整数N除以正整数m后的余数为n”记为N≡n(modm),例如8≡2(mod3).执行如图的该程序框图后,输出的i值为( )
把“正整数N除以正整数m后的余数为n”记为N≡n(modm),例如8≡2(mod3).执行如图的该程序框图后,输出的i值为( )| A. | 14 | B. | 17 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1} | B. | {x|x>1} | C. | {x|x<-1或x>1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 1或-3 | C. | 1 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com