
分析 (1)分别设出P、M的坐标,由已知把M的坐标用P得坐标表示,再把M的坐标代入圆的方程得答案;
(2)设出直线l的方程,联立直线方程和椭圆方程,由判别式等于0得到m2=4k2+1,由点到直线的距离公式求得原点O到直线l的距离d,写出△QAB面积,利用基本不等式求得最值,并得到△QAB面积取最大值时的d值,可得m2=2k2+2.与m2=4k2+1联立求得k,m的值,则直线方程可求.
解答 解:(1)设P(x,y),M(x0,y0),则D(x0,0),
∵P与点Q关于原点O对称,
∴$\overrightarrow{QP}=2\overrightarrow{OP}$,从而$2\overrightarrow{OP}=\overrightarrow{OM}+\overrightarrow{OD}$,即2(x,y)=(x0,y0)+(x0,0)=(2x0,y0).
∴$\left\{\begin{array}{l}{x={x}_{0}}\\{2y={y}_{0}}\end{array}\right.$,代入${{x}_{0}}^{2}+{{y}_{0}}^{2}=4$,得x2+4y2=4.
即$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)当直线l的斜率不存在时,不合题意,故设l:y=kx+m.
联立$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,得(1+4k2)x2+8kmx+4m2-4=0.
∵l与椭圆相切,
∴△=16(4k2+1-m2)=0,得m2=4k2+1,①
原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,则$|AB|=2\sqrt{4-{d}^{2}}$,
∴△QAB面积S=$\frac{1}{2}|AB|•2d=2d\sqrt{4-{d}^{2}}=2\sqrt{{d}^{2}}•\sqrt{4-{d}^{2}}≤{d}^{2}+4-{d}^{2}=4$.
当且仅当d2=4-d2,即d=$\sqrt{2}$时,△QAB面积有最大值4.
此时$d=\frac{|m|}{\sqrt{1+{k}^{2}}}=\sqrt{2}$.即m2=2k2+2.②
联立①②解得$k=±\frac{\sqrt{2}}{2},m=±\sqrt{3}$.
∴直线l的方程为:$y=\frac{\sqrt{2}}{2}x+\sqrt{3}$或$y=\frac{\sqrt{2}}{2}x-\sqrt{3}$或$y=-\frac{\sqrt{2}}{2}x+\sqrt{3}$或$y=-\frac{\sqrt{2}}{2}x-\sqrt{3}$.
点评 本题考查椭圆方程的求法,训练了利用代入法求切线方程,考查直线与圆锥曲线位置关系的应用,考查利用基本不等式求最值,属中档题.


科目:高中数学 来源: 题型:填空题
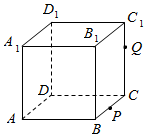 如图所示,正方体ABCD-A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点,过点A、P、Q的平面截正方体所得的截面即为S.
如图所示,正方体ABCD-A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点,过点A、P、Q的平面截正方体所得的截面即为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}∈A$ | B. | $\sqrt{11}∈A$ | C. | $\sqrt{7}∈A$ | D. | 4∈A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
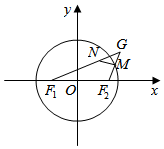 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),点M是圆x2+y2=4上的动点,动点G满足$\overrightarrow{{F}_{2}M}$=$\overrightarrow{MG}$,过点M作直线l⊥F2G并交直线F1G于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com